1. Recursie
Bekijk nog eens opnieuw het algoritme van Euclides uit deel 1. We kunnen dit ook op in code omzetten waarbij we extra code hebben toegevoegd om het algoritme nog eens te demonsteren:
public class Euclids {
/**
* return de gcd
*
* @param biggest
* @param smallest
* @return
*/
public int gcd(int biggest, int smallest) {
if (smallest > 0) {
System.out.print("gcd(" + smallest + " ," + biggest % smallest + ") omdat ");
System.out.println(biggest + " = " + (biggest / smallest) + " x " + smallest + " + " + biggest % smallest);
}
if (smallest == 0) {
//het deelgetal is de GGD.
return biggest;
}
//Zolang de rest ongelijk is aan 0, deel het grootste getal door het kleinste getal en neem daarvan de restwaarde
return gcd(smallest, biggest % smallest);
}
public static void main(String[] args) {
Euclids euclids = new Euclids();
System.out.println("Conclusie: de ggd van 1140 en 900 is: " + euclids.gcd(1140 , 900) + "\n");
System.out.println("Conclusie: de ggd van 730 en 245 is: " + euclids.gcd(730, 245) + "\n");
System.out.println("Conclusie: de ggd is: 752 en 372 " + euclids.gcd(752, 372) + "\n");
}
}
Wat gebeurt hierboven? In de regel return gcd(smallest, biggest % smallest); roept de methode zichzelf aan. We noemen dit recursie. We kunnen dat ook nog wat eenvoudiger opschrijven:
geef terug ggd(grootste getal, kleinste getal):
als het grootste getal gelijk is aan 0
dan is het antwoord: het grootste getal
anders
is het antwoord: roep opnieuw aan ggd(kleinste getal, (grootste getal mod kleinste getal))
Ter herinnering mod staat voor modulo (geheel getal) rekenen en geeft de restwaarde terug. Bijvoorbeeld 5 mod 3 = 2 omdat 3 één keer in 5 past.
Bij recursie zit er altijd een stop in de recursie. Dit gebeurt in het volgende stukje code:
if (smallest == 0) {
//het deelgetal smallest is de GGD.
return biggest;
}
Er komt een punt waarop er geen restwaarde meer is en dan is het deelgetal gevonden.
2. De faculteit van een getal
Een andere vorm van recursie kunnen we vinden in de faculteit van een getal. De faculteit van 4 is:
4! = 4 * 3 * 2 * 1 = 24
Je kunt dat ook anders opschrijven:
4! = n * (n-1) * (n-2) * (n-3) = 24 waarbij n staat het getal waarvan de faculteit moet worden uitgerekend.
Je kunt ook zeggen dat 4! hetzelfde is als 4 * 3! en dat 3! hetzelfde is als 3 * 2! en 2! En dat is hetzelfde als 1! * 1 en 1! hetzelfde is als 0! x 1. Dat is niet 0 omdat er een afspraak is dat 0!=1. De uitkomst van 0! x 1 is dus 1. Omdat we dit nu weten kunnen we ook 1! uitrekenen dat is namelijk 1 x 0! = 1 x 1 = 1. Hierna kunnen we 2! uitrekenen namelijk 2 x 1! = 2 x 1 = 2. En hierna kunnen we 3! uitreken namelijk 3 x 2! = 3 x 2! = 6 en zo komen we bij 4! = 4 x 6 = 24.
Hetzelfde gebeurt bij onderstaande code:
public int factorial(int fact) {
if (fact == 0) {
return 1;
}
return factorial(fact - 1) * fact;
}
De eerste keer wordt n * (n-1)! berekend. Maar omdat we niet weten wat (n-1)! berekenen we (n-2)! en daarna (n-3)!. Al deze berekeningen worden op de stack geplaatst en daarna met elkaar vermenigvuldigd.
De stack
De stack die kennen we al. Nu wordt deze bij recursie gebruikt. Stel we roepen factoral(4) aan. Omdat we niet weten hoeveel factorial(4) is wordt deze op de stack geplaatst.
In de volgende ronde gaan we we eerst uitrekenen wat factorial(3) is maar ook deze berekening kunnen we nog niet uitvoeren dus wordt deze op de stack geplaatst.
|
|
|
| factorial(3) |
| factorial(4) |
Ook factorial(2) wordt op de stack geplaatst en daarna factorial (1) en uiteindelijk komen we bij 0. De stack is nu volledig gevuld.
| factorial(0) |
| factorial(1) |
| factorial(2) |
| factorial(3) |
| factorial(4) |
Factorial(0) kunnen we uitrekenen. Bij fact ==0 wordt 1 teruggegeven. Deze wordt ook weer van de stack gepopt.
|
| factorial(1) |
| factorial(2) |
| factorial(3) |
| factorial(4) |
Factorial(1) kunnen we nu ook uitrekenen en dat wordt 1. Deze wordt ook van de stack gepopt.
|
|
| factorial(2) |
| factorial(3) |
| factorial(4) |
En op dezelfde manier wordt factorial(2), factorial(3) van de stack gepopt en uiteindelijk factorial(4). De laatste geeft uiteindelijk de uitkomst terug.
Je ziet dat het heel belangrijk is dat factorial(0) terug geeft. Zonder deze stop zouden we een zogenaamde stack overflow geven omdat er maar factorials op de stack worden geplaats.
Exception in thread "main" java.lang.StackOverflowError
at datastructuren.Fact.factorial(Fact.java:18)
at datastructuren.Fact.factorial(Fact.java:18)
at datastructuren.Fact.factorial(Fact.java:18)
at datastructuren.Fact.factorial(Fact.java:18).....
3. De torens van Hanoi
De Torens van Hanoi is een spel of puzzel met een aantal schijven. Het verhaal gaat over een Indiase tempel in een stad genaamd Kashi Vishwanath waarin een gebouw staat met bevat met drie palen omringd door 64 gouden schijven. Priesters hebben de schijven volgens de regels van Brahma verplaatst. De puzzel is daarom ook bekend als de puzzel van de Toren of Brahma. Volgens deze legende zal de wereld ten onder gaan als de laatste zet van de puzzel is voltooid.
De regels van Brahma zijn:
- Er mag slechts 1 schijf tegelijk worden verplaatst.
- Deze wordt altijd van bovenaf gepakt.
- Er mag nooit een grotere schijf op een kleinere worden geplaatst.
- Alle schijven moeten uiteindelijk op de doeltoren worden geplaatst.

Bezoekers van een museum bezig met de puzzel.
Als deze legende waar is en als de priesters de schijven met een snelheid van één per seconde hebben kunnen verplaatsen duurt het ongeveer 584 miljard jaar om de puzzel op te lossen. Dus gelukkig, we hebben nog even. Ter vergelijking: het heelal is 13,8 miljard jaar oud en de zon ongeveer 4,6 miljard jaar. De zon kan maximaal 10 miljard jaar worden dus tegen die tijd is inderdaad de aarde ten einde.
Het spel bestaat uit een plankje met daarop drie stokjes. Bij aanvang van het spel is op een van de stokjes een kegelvormige toren geplaatst van schijven met een gat in het midden. De schijven hebben verschillende diameters, in toenemende grootte. Ze zijn zo geplaatst dat de kleinste schijf bovenop en de grootste onderop ligt.

Het doel van het spel is om de complete toren van schijven te verplaatsen naar een ander stokje volgens de regels van Brahma.
We beginnen zullen dat demonstreren met een puzzel van 3 schijven. We geven eerst alle torens een naam. De begintoren noemen we A. De middelste toren noemen we B en de doeltoren C.

We gaan nu het volgende algoritme uitvoeren:
Verschuif disk 1 van toren A naar toren C:
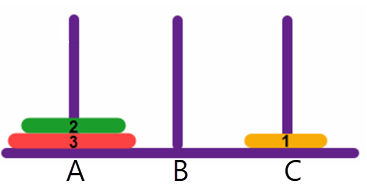
Verschuif disk 2 van toren A naar toren B:
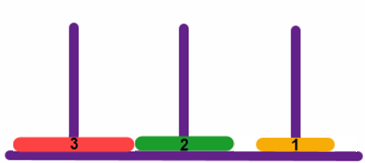
Verschuif disk 1 van toren C naar toren B:
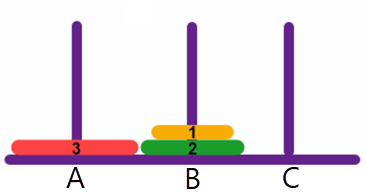
Verschuif disk 3 van toren A naar toren C:
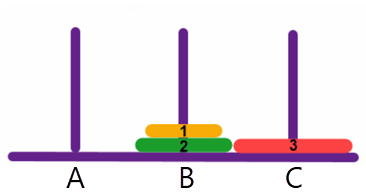
Verschuif disk 1 van toren B naar toren A:
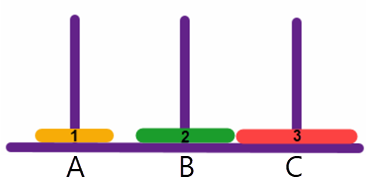
Verschuif disk 2 van toren B naar toren C:
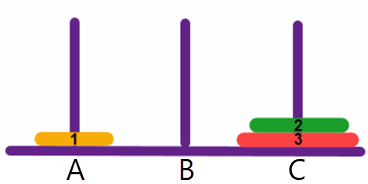
Verschuif disk 1 van toren A naar toren C...:
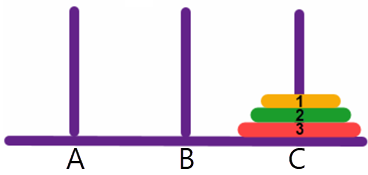
..en het is gedaan. Moeilijk is deze oplossing niet maar hoe vertalen we dat nu in een algoritme? We zullen nu aantonen dat recursie de eenvoudigste oplossing is. Bedenk hierbij dat we dan telkens bovenstaande stappen uitvoeren, ongeacht het aantal schijven.
public class Hanoi {
public void sorteerTorens(int top, char van, char tussen, char doel) {
if (top == 1) {
} else {
sorteerTorens(top - 1, van, doel, tussen);
sorteerTorens(top - 1, tussen, van, doel);
}
}
public static void main(String[] args) {
Hanoi hanoi = new Hanoi();
hanoi.sorteerTorens(3, 'A', 'B', 'C');
}
}
In deze code wordt het printen van de oplossing niet gegeven. Dit komt in de bijbehorende opdracht. Merk op dat de 2e en de 3e disk telkens op een bepaalde manier wordt gesorteerd (daarna de 3e en de 4e etc.) en merk ook op dat de oplossing in omgekeerde volgorde wordt weergegeven. Hier herkennen we weer de stack.
4. Merge sort op 2 gesorteerde arrays
We zullen nu aantonen dat recursie uitermate geschikt is om te sorteren. We zullen dit doen met het algoritme Merge sort wat het best in het Nederlands vertaald kan worden als "voeg de sorteringen samen". Het werkt als volgt:
Stel dat we 2 gesorteerde arrays hebben gemaakt:
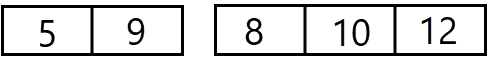
We kunnen dit als volgt sorteren. We plaatsen de cursor aan het begin van de 2 arrays:

We vergelijken deze twee getallen met elkaar en plaatsen het kleinste op een nieuwe array:
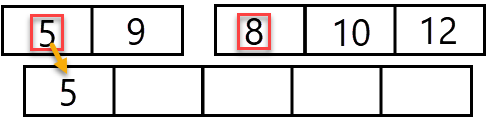
Vervolgens verplaatsen we de cursor van de array van het kleinste getal één getal verder:
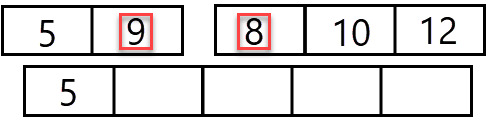
We vergelijken deze getallen opnieuw met elkaar en plaatsen wederom het kleinste getal op de nieuwe array. Tevens verplaatsen we de cursor, nu van de array aan de rechterkant:
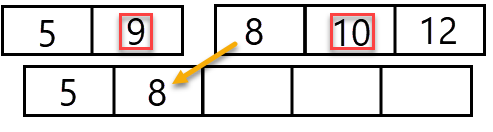
Nu vergelijken we weer getal 9 en 10 met elkaar - 9 wordt op de nieuwe array geplaatst en als laatste plaatsen we getal 10 en 12 omdat deze niet meer te vergelijken zijn:
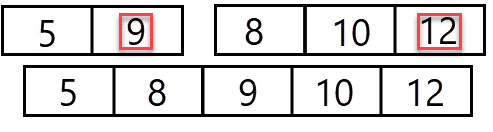
5. Merge sort op een ongesorteerde array
Wat nu als de array niet is gesorteerd? Dan gaan we deze eerst opsplitsen in 2 array:
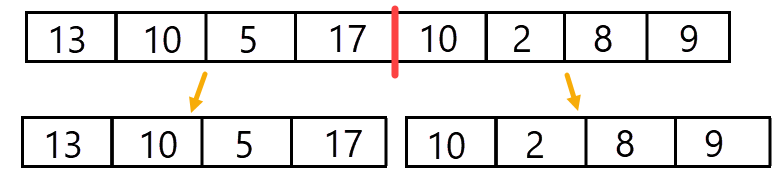
Hierna splitsen we opnieuw op:
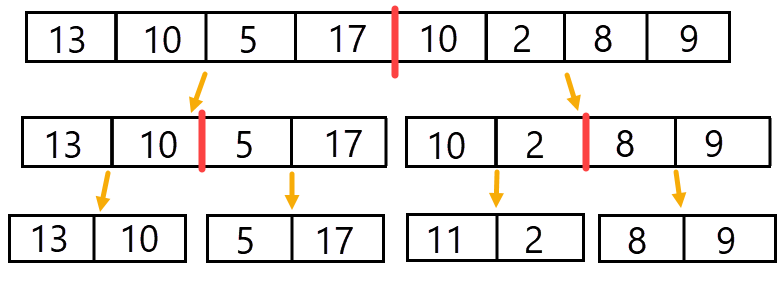
En nu zie je dat de vier ontstane arrays nog steeds niet gesorteerd zijn. Dan gaan we door tot 8 arrays van een enkel nummer:
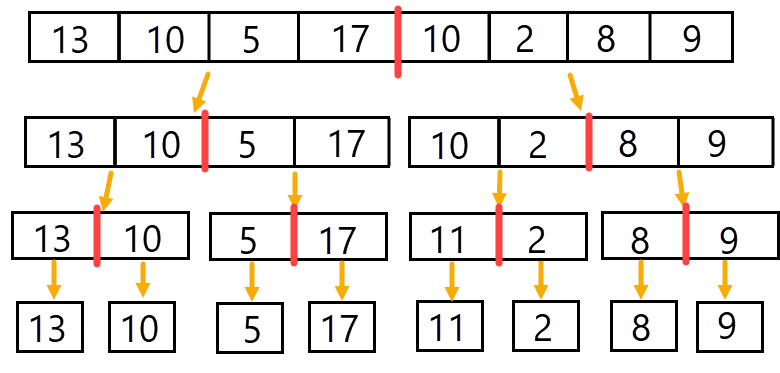
We kunnen nu stellen dat elk van de 8 arrays is gesorteerd, ook als zit er maar één element in. Hier kunnen we vervolgens het eerder uitgelegde algoritme op los laten.
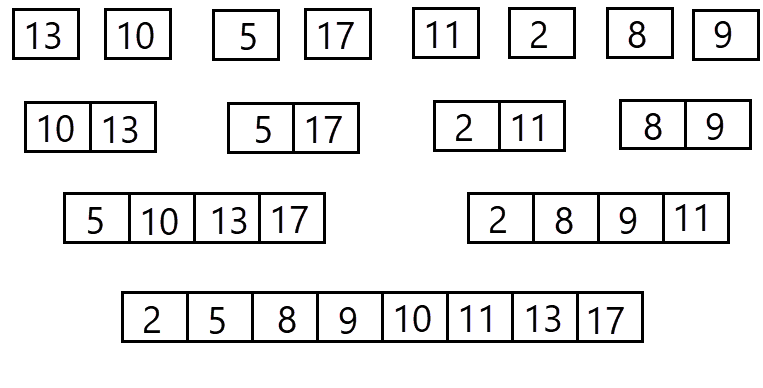
6. Merge sort in code
We zullen nu de code gaan maken. Deze is gebaseerd op de volgende code:
/**
* In dit deel wordt de array gesplitst tot uiteindelijk arrays van 1 element
*
* @param start
* @param end
*/
mergeSort(int start, int end)
en
/**
* Deze methode checkt op basis van de index twee getallen en verwisseld deze indien nodig
* @param low
* @param middle
* @param high
*/
merge(int low, int middle, int high)
Grafisch kunnen we dit nu als volgt voorstellen. Met mergesort wordt de array opgesplitst in arrays van één element en vervolgens weer gesorteerd samengevoegd.
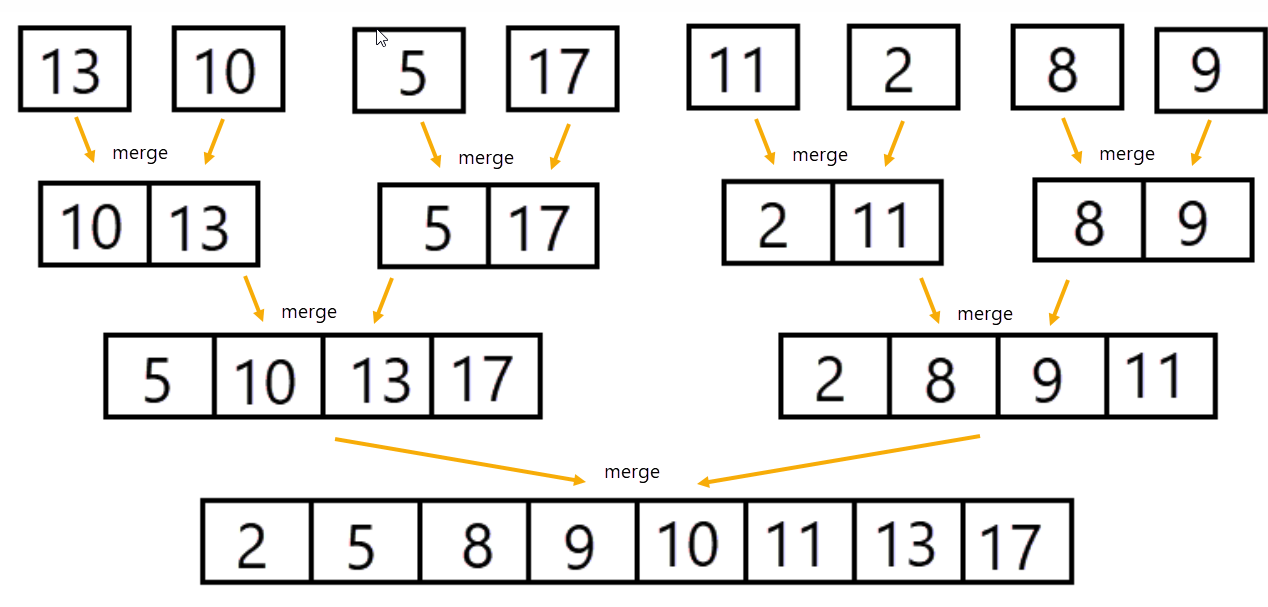
We zullen dat nu demonstreren met een array van vier elementen [8, 3, 4, 0]. We voeren hierop de volgende code uit:
mergeSort (0, 1).
Hiermeee wordt de volgende array gemaakt: [8, 3]. Omdat deze array niet is gesorteerd wordt de methode op de stack geplaatst.
Vervolgens wordt de volgende methode uitgevoerd.
mergeSort (0, 0).
Dit geeft de array van element: [8]
Nu de wordt de volgende methode op de stack geplaatst: mergeSort (1, 1) en deze geeft een array met het element [3]
De "splitscursor" wordt daarbij na het 1e getal geplaatst: [8 | 3, 4, 0]
De 2 arrays worden gewisseld: [8]<=> [3] en daarna samengevoegd (terug geplaatst in de helparray).
De helparray is nu: [3, 8, 4, 0] en de index wordt verhoogd naar na het 2e getal: [8, 3 | 4, 0] en vervolgens wordt er gekeken naar de rechterkant van de array.
In de onderstaande, volledige, code kun je het zien gebeuren. We maken met behulp van een Random generator telkens een nieuwe array.
import static java.lang.Math.floor;
import java.util.Arrays;
import java.util.Random;
public class Mergesort {
private int[] numbers;
private int[] helpArray;
private int length;
/**
* sort the array
*
* @param values
*/
public void sort(int[] values) {
this.numbers = values;
length = values.length;
this.helpArray = new int[length];
mergeSort(0, length - 1);
}
/**
* In dit deel wordt de array gesplitst tot uiteindelijk arrays van 1
* element
*
* @param start
* @param end
*/
private void mergeSort(int start, int end) {
//als start kleiner is dan end dan zijn er nog steeds meerdere elementen
if (start < end) {
// Bepaal het midden van de array
int middle = (int) floor((start + end) / 2);
//Sorteer de linkerkant van de array
System.out.print("Op de stack wordt geplaatst (links): ");
System.out.println("mergeSort (" + start + ", " + middle + ")");
mergeSort(start, middle);
//Sorteer de rechterkant van de array
System.out.print("Op de stack wordt geplaatst (rechts) : ");
System.out.println("mergeSort (" + (middle + 1) + ", " + end + ")");
mergeSort(middle + 1, end);
//En combineer nu beiden
//System.out.println("merge(" + start + ", " + middle + ", " + end + ")//Combineer beiden");
merge(start, middle, end);
System.out.println("De array is nu: " + Arrays.toString(numbers));
}
}
/**
* Deze methode checkt op basis van de index twee getallen en verwisseld deze indien nodig
* @param low
* @param middle
* @param high
*/
private void merge(int low, int middle, int high) {
//plaats de array in een helper array
for (int i = low; i <= high; i++) {
helpArray[i] = numbers[i];
}
int lowest1 = low;
int middelPlusOne = middle + 1;
int lowest2 = low;
//in dit
while (lowest1 <= middle && middelPlusOne <= high) {
if (helpArray[lowest1] <= helpArray[middelPlusOne]) {
numbers[lowest2] = helpArray[lowest1];
lowest1++;
} else {
System.out.println("\nDe array wordt gesplitst na het " + (middelPlusOne) + "e getal...");
System.out.println("Deze 2 getallen worden gewisseld: " + helpArray[lowest2] + " <=> " + helpArray[middelPlusOne]);
numbers[lowest2] = helpArray[middelPlusOne];
middelPlusOne++;
System.out.println("De index wordt verhoogd naar na het " + (middelPlusOne) + "e getal. ");
}
lowest2++;
}
//maak de nieuwe array
while (lowest1 <= middle) {
numbers[lowest2] = helpArray[lowest1];
lowest2++;
lowest1++;
}
}
public static void main(String[] args) {
int[] numbersArray = new int[4];
Random generator = new Random();
for (int i = 0; i < numbersArray.length; i++) {
numbersArray[i] = generator.nextInt(20);
}
Mergesort sorter = new Mergesort();
System.out.println(Arrays.toString(numbersArray));
sorter.sort(numbersArray);
System.out.println("De array is gesorteerd: " + Arrays.toString(numbersArray));
}
}
7. antwoorden
Dit onderdeel is uitgeschakeld door de docent.

