1. De ontwikkeling van programmeertaal
De bouw van machines om wiskundige berekeningen te maken, startte al vroeg met de Abacus. Het zal echter tot 1936 duren eer dat er een daadwerkelijke bruikbare computer wordt gebouwd. In opdracht 2.1 ga je zelfstandig aan de slag met een overzicht van de geschiedenis van de computer.
Met de komst van het binaire systeem werden ook de programmeertalen geïntroduceerd. De eerste taal die werd ontwikkeld was imperatief. Dat had te maken met de architectuur van de computer. Een imperatieve taal kenmerkt zich doordat alle instructies van boven naar beneden worden gelezen. Hieronder zie je een stukje van de imperatieve programmeertaal C.
c = 1 + 3;
d = c;
c++;
printf(c+d);
Met de komst van het programeren doen tevens twee begrippen hun intrede: geheugen en functies. Functies spelen ook in de wiskunde een centrale rol. Ze leggen een verband tussen de invoer en de uitvoer en kunnen tevens dienen als een black box.
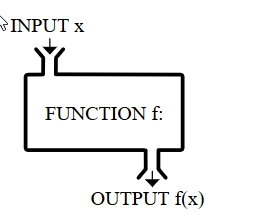
Omdat computertijd vroeger heel duur was maar tegenwoordig steeds goedkoper en sneller ontwikkeld de programmeertaal zich meer en meer richting menselijke belevingswereld. Haskell is een voorbeeld van een taal wat zich meer richting de menselijke belevingswereld heeft ontwikkelde. We noemen dit een functionele programmeertaal. Desalniettemin zal het in eerste instantie toch vrij abstract overkomen mede omdat het programmeren via de commandprompt gaat.
In onderstaande Prezi presentatie geven we een overzicht van de geschiedenis van de computer. De theoretische basis voor het imperatief programmeren is in de jaren dertig gelegd door wetenschappers zoals Alan Turing en John voin Neumann. De theorie van functies begint al in 1777 bij Leonhard Euler. Hij voerde bijvoorbeeld het gebruik van de Griekse letter π in als verhouding van de omtrek van de cirkel tot zijn middellijn. Het zou tot 1950 duren voordat iemand op het idee kwam om deze functie-theorie te gebruiken als basis voor het programmeren.
Ga naar de Prezi op prezi.com.
2. Wat is Haskell
De basis van deze cursus is de website http://learnyouahaskell.com/ . We hebben geprobeerd deze cursus zo begrijpelijk mogelijk te maken voor leerlingen uit het voortgezet onderwijs.
Haskell is een functionele programmeertaal. Dat is wat anders dan een imperatieve of procedurele programmeertaal. Een voorbeeld hiervan is als volgt (in de taal C):
a = 1 + 2; //geef variabele a de waarde 1 + 2
c=1; //geef variabele c de waarde 1
b=a; //geef variabele b de waarde van variabele a
c++; //hoog c op met 1
printf(a+b+c); //print de opgetelde waarden van de drie variabelen naar het scherm
Vaak wordt als tegenhanger van imperatief programmeren het object geörienteerd programmeren (ook wel aangeduid als OO-programmeren). Voorbeeldenvan OO-programmeren vind je in de cursus een interactieve applicatie. Een voorbeeld van een bekendere functionele programmeertaal is Javascript.
wiskunde
De taal Haskell zit heel dicht tegen de wiskunde aan. Neem bijvoorbeeld de volgende wiskundige functie:
y = x2 + 3x
Tegenwoordig wordt dit ook opgeschreven als
f(x) = x2 + 3x
We kunnen zeggen de functie f met x als input. De parameter x noemen we dan een argument of een invoer.
In Haskelll wordt deze functie als volgt gemaakt:
f x = x*x + 3*x
Meer parameters kan ook
f(x,y) = x2 + 3y + 2
Haskell:
f x y = x*x + 3*y + 2
We kunnen zelfs de functie f weer in een nieuwe functie opnemen.
3. Software installeren
Voor deze cursus gaan we werken met een Haskell compiler. Deze is te downloaden op http://hackage.haskell.org/platform/. Neem de minimale versie en let erop of je een 32-bit of 64-bit computer hebt. Dit is te vinden door in verkenner op Deze pc (afhankelijk van je windows versie)
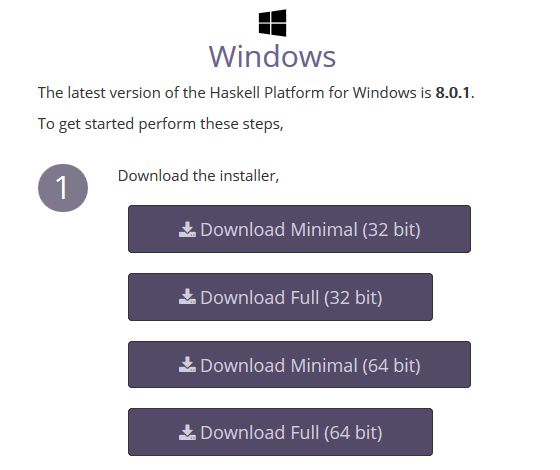
Hierna kun je een aantal keren op next klikken om de compiler te installeren. Het kan even duren eer het klaar is.
Als het programma is geïnstalleerd open je een terminal window. In de opdrachtprompt kun je de compiler starten door ghci in te typen. Wij zullen vanaf nu met deze prompt werken. Je bent echter vrij om de standaard prompt te gebruiken.
GHCi, version 8.0.1: http://www.haskell.org/ghc/ :? for help
Prelude> :set prompt "ghci> "
ghci>
GHCI staat voor The Glasgow Haskell Compiler. Een compiler is een computerprogramma dat een in een brontaal geschreven programma vertaalt in een equivalent programma van de doeltaal.
4. Je eerste code in Haskell
We zullen nu eerste code uitproberen. Haskell kan functioneren als een rekenmachine. Probeer de volgende berekeningen maar eens uit:

Je kunt ook werken met negatieve getallen. Je zult hierbij echter wel moeten werken met haken want anders krijg je een Precedence parcing error.

Haskell geeft hier heel duidelijk aan wat er aan de hand is:
cannot mix `*' [infixl 7] and prefix `-' [infixl 6] in the same infix expression
Tussen haken gaat het dus wel goed.
5. True en False
Het booleaanse rekenen is allemaal niet zo spannend

6. Functies in Haskell
Zonder dat je het wist heb je al diverse functies uitgevoerd. De + en de * noemen we infix functies. Dit zegt iets over de manier van opschrijven. Normaal gesproken wordt een functie prefix opgeschreven. Voorbeeld f(x , y). We schrijven niet +(3, 4) maar 3 + 4 of 3 * 4. Dat noemen we infix.
Prefixnotatie is omstreeks 1920 uitgevonden door de Poolse logicus Jan Lukasiewicz als notatie voor de propositielogica. Men spreekt daarom ook wel van Poolse notatie.
Een prefix functie in Haskell is de volgende
ghci> max 7 10
10
ghci> min 3 7
3
In het vorige onderdeel vond je al voorbeelden van infix functies. Een iets gebruikelijkere term voor een infix functie is een operator. Je kunt een prefix functie omzetten naar een infix functie door middel van back quotes. De functie quot geeft van een deling een geheel getal terug.
ghci> quot 23 3
7
ghci> 23 `quot` 3
7
7. Een functie zelf maken
Haskell kent een aantal ingebouwde functies zoals :load, :edit of :type. Het is ook mogelijk om zelf functies te maken. Dit gebeurt in een apart bestand. Om dit te maken open je eerst het programma Netbeans. Hierin maak je een zogenaamde empty file.
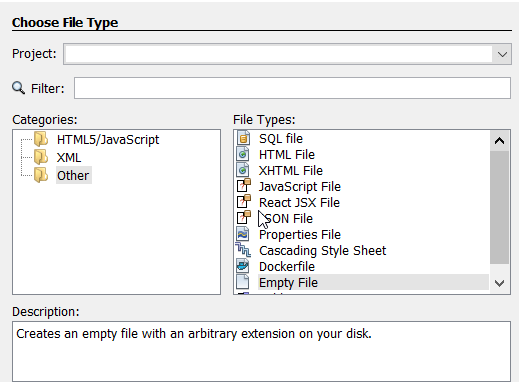
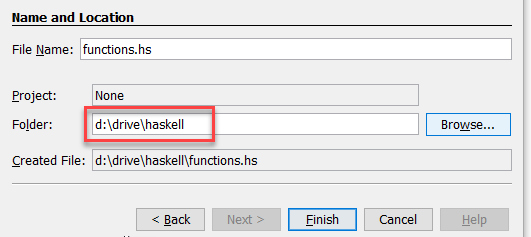
Geef de file de naam functions.hs.
Tevens kun je met de cmd-prompt (of met verkenner) het beste even ergens een mapje aanmaken. Bij ons staat het mapje op de D: drive en dit is tevens de drive van Google Drive zodat we meteen een backup hebben.
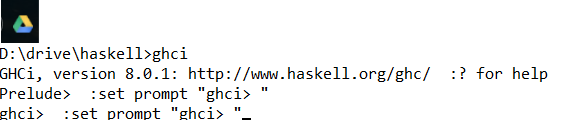
Het bestand functions.hs slaan we op in deze map.
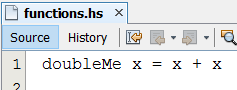
In Netbeans maken we de functie DoubleMe. Merk op dat een functie niet wordt afgesloten met een ; of iets dergelijks. Sla de file opnieuw op met Ctrl-s.
eVrvolgens kun je dit bestand inladen met het commando :load.
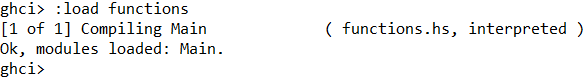
En nu ben je in staat om de functie uit te voeren. De functie vraagt 1 argument.
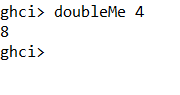
Een tweede functie
Je kunt ook een tweede functie maken. Breidt je script uit met de volgende functie.
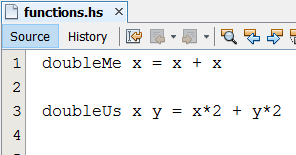
Als je het script opnieuw inlaadt kun je de functie gebruiken.
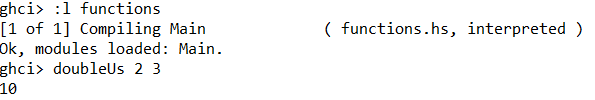
Je kunt functies ook overnieuw gebruiken wat overzichtelijkere code oplevert.
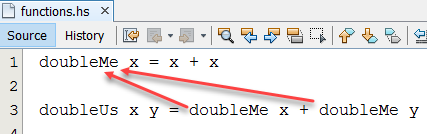
Nog een paar dingen over functies.
- Functies mogen niet met een hoofdletter beginnen.
- Als het een stukje code is wat iets teruggeeft (retourneert) dan noemen we dat een expressie. De expressie x + x geeft een dubbele x terug.
- Een functie heeft doorgaans een of meerdere argumenten of parameters. Als een functie geen argumenten heeft dan noemen we dat een definitie. Een voorbeeld van een defintie is
myName = "Piet Klaassen"
8. lijsten
In Haskell wordt veel gebruikt gemaakt van lijsten. Een lijst is vergelijkbaar met een array in Java. Het ziet er als volgt uit.
[4,8,15,16,23,42]
Je kunt zo'n lijst ook een naam geven met het commando let. Dit maakt de code overzichtelijker.
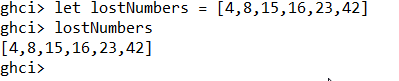
Op lijsten kun je allerlei functies toepassen zoals de som.
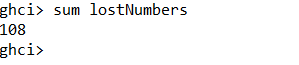
Je kunt lijsten ook aaneenschakelen.
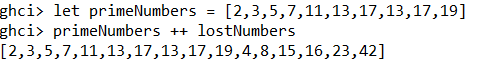
Dit noemen we een concatenate
Dit kan niet.

Dit komt omdat een lijst homogeen dient te zijn. Je kunt er óf integers in opslaan óf characters.
9. Een lijst in een lijst
Een lijst in een lijst opslaan kan ook.
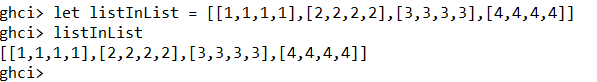
Hier kun je wat technieken op loslaten. Stel je hebt een lijst met 4 nummers 5 en je wilt deze toevoegen aan listInList.
Eerst maak je deze lijst aan en daarna probeer je deze toe te voegen met het concanate symbool ++.

Er onstaat dan een non type-variable foutmelding. Met andere woorden: haskell verwacht een argument van hetzelfde type. Dat moet dus ook een lijst in een lijst zijn.
10. Functies op een lijst
We kunnen nog wat belangrijke functies toepassen op een lijst.
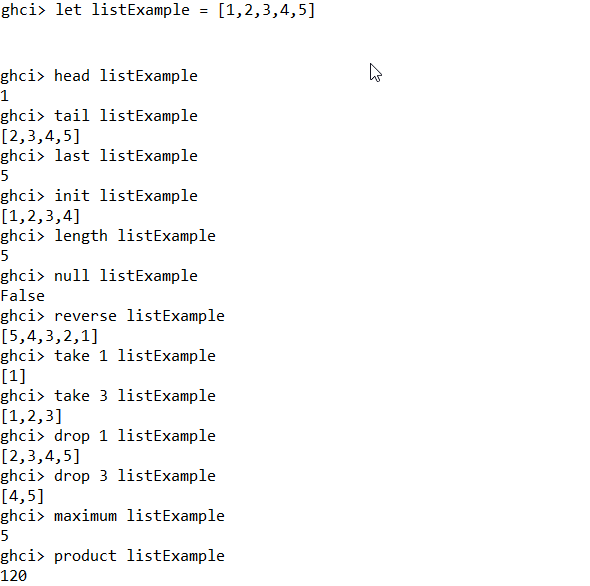
Tot slot van dit lesonderdeel nog een wat geavanceerdere functie. Stel dat we de volgende code uitvoeren.

Je ziet dat we ook op deze manier een lijst kunnen samenstellen. Deze manier van definiëren is rechtstreeks gekoppeld aan de wiskunde. Het "|"-teken noemen we the pipe. Na de pipe gebeurd er niets anders dan in de variabele names drie namen stoppen. We kunnen dit echter ook combineren met een concenate teken.

Je ziet dat er nu een combinatie wordt gemaakt tussen de eerste en de tweede lijst. Het resultaat zijn alle combinaties.
De volgende code ligt dan voor de hand.

11. Tuples
Soms is het nodig om data te groeperen met verschillende soorten type data. Hiervoor kunnen we een tuple nemen:
ghci> ("Jan", True, 2)
("Jan",True,2)
Je ziet dat het mogelijk is om drie verschillende type data bij elkaar te plaatsen. Als we het type opvragen, geeft Haskell de drie verschillende soorten terug:
:t ("Jan", True, 2)
("Jan", True, 2) :: Num t => ([Char], Bool, t)
We kunnen tuples ook in een lijst bewaren:
ghci> let tuple = ("Jan", True, 2)
ghci> let tuple2 = ("Kees", False, 3)
ghci> let list = [tuple, tuple2]
ghci> list
[("Jan",True,2),("Kees",False,3)]
Als we echter een derde tuple met een andere samenstelling hier aan toe willen voegen geeft Haskell een foutmelding:
ghci> let tuple 3 = ("Marie",False,"drie")
ghci> let list = [tuple, tuple2, tuple3]
<interactive>:14:20: error:
* Couldn't match expected type `a -> ([Char], Bool, [Char])'
with actual type `([Char], Bool, Integer)'
* In the expression: tuple2
In the expression: [tuple, tuple2, tuple3]
In an equation for `list': list = [tuple, tuple2, tuple3]
* Relevant bindings include
list :: [a -> ([Char], Bool, [Char])] (bound at <interactive>:14:5)
Een toepassing van een tuple
Stel dat we een driehoek willen vastleggen. Een driehoek heeft drie zijden; a, b en c. Deze zijn van het type Number.
Dit kunnen we als volgt definiëren:
ghci> let triangle = (1,2,3)
ghci> :t triangle
triangle :: (Num t2, Num t1, Num t) => (t, t1, t2)
Het is een driehoek met zijden a=1, b=2, c=3.
Stel nu dat we een alle mogelijke driehoeken met zijden (a,b,c) kleiner of gelijk dan 10 in een definitie vastleggen en daarna tonen.
let triangles = [ (a,b,c) | a <-[1..10], b <-[1..10], c<-[1..10]]
ghci> triangles
[(1,1,1),(1,1,2),(1,1,3),(1,1,4),(1,1,5),(1,1,6),(1,1,7),(1,1,8),(1,1,9),(1,1,10),(1,2,1),(1,2,2),(1,2,3),(1,2,4),(1,2,5),(1,2,6),(1,2,7),(1,2,8),(1,2,9),(1,2,10),(1,3,1),(1,3,2),(1,3,3),(1,3,4),(1,3,5),(1,3,6),(1,3,7),(1,3,8),(1,3,9),(1,3,10),(1,4,1),(1,4,2),(1,4,3),(1,4,4),(1,4,5),(1,4,6),(1,4,7),(1,4,8),(1,4,9),(1,4,10),(1,5,1),(1,5,2),(1,5,3),(1,5,4),(1,5,5),(1,5,6),(1,5,7),(1,5,8),(1,5,9),(1,5,10),(1,6,1),(1,6,2),(1,6,3),(1,6,4),(1,6,5),(1,6,6),(1,6,7),(1,6,8),(1,6,9),(1,6,10),(1,7,1),(1,7,2),(1,7,3),(1,7,4),(1,7,5),(1,7,6),(1,7,7),(1,7,8),(1,7,9),(1,7,10),(1,8,1),(1,8,2),(1,8,3),(1,8,4),(1,8,5),(1,8,6),(1,8,7),(1,8,8),(1,8,9),(1,8,10),(1,9,1),(1,9,2),(1,9,3),(1,9,4),(1,9,5),(1,9,6),(1,9,7),(1,9,8),(1,9,9),(1,9,10),(1,10,1),(1,10,2),(1,10,3),(1,10,4),(1,10,5),(1,10,6),(1,10,7),(1,10,8),(1,10,9),(1,10,10),(2,1,1),(2,1,2),(2,1,3),(2,1,4),(2,1,5),(2,1,6),(2,1,7),(2,1,8),(2,1,9),(2,1,10),(2,2,1),(2,2,2),(2,2,3),(2,2,4),(2,2,5),(2,2,6),(2,2,7),(2,2,8),(2,2,9),(2,2,10),(2,3,1),(2,3,2),(2,3,3),(2,3,4),(2,3,5),(2,3,6),(2,3,7),(2,3,8),(2,3,9),(2,3,10),(2,4,1),(2,4,2),(2,4,3),(2,4,4),(2,4,5),(2,4,6),(2,4,7),(2,4,8),(2,4,9),(2,4,10),(2,5,1),(2,5,2),(2,5,3),(2,5,4),(2,5,5),(2,5,6),(2,5,7),(2,5,8),(2,5,9),(2,5,10),(2,6,1),(2,6,2),(2,6,3),(2,6,4),(2,6,5),(2,6,6),(2,6,7),(2,6,8),(2,6,9),(2,6,10),(2,7,1),(2,7,2),(2,7,3),(2,7,4),(2,7,5),(2,7,6),(2,7,7),(2,7,8),(2,7,9),(2,7,10),(2,8,1),(2,8,2),(2,8,3),(2,8,4),(2,8,5),(2,8,6),(2,8,7),(2,8,8),(2,8,9),(2,8,10),(2,9,1),(2,9,2),(2,9,3),(2,9,4),(2,9,5),(2,9,6),(2,9,7),(2,9,8),(2,9,9),(2,9,10),(2,10,1),(2,10,2),(2,10,3),(2,10,4),(2,10,5),(2,10,6),(2,10,7),(2,10,8),(2,10,9),(2,10,10),(3,1,1),(3,1,2),(3,1,3),(3,1,4),(3,1,5),(3,1,6),(3,1,7),(3,1,8),(3,1,9),(3,1,10),(3,2,1),(3,2,2),(3,2,3),(3,2,4),(3,2,5),(3,2,6),(3,2,7),(3,2,8),(3,2,9),(3,2,10),(3,3,1),(3,3,2),(3,3,3),(3,3,4),(3,3,5),(3,3,6),(3,3,7),(3,3,8),(3,3,9),(3,3,10),(3,4,1),(3,4,2),(3,4,3),(3,4,4),(3,4,5),(3,4,6),(3,4,7),(3,4,8),(3,4,9),(3,4,10),(3,5,1),(3,5,2),(3,5,3),(3,5,4),(3,5,5),(3,5,6),(3,5,7),(3,5,8),(3,5,9),(3,5,10),(3,6,1),(3,6,2),(3,6,3),(3,6,4),(3,6,5),(3,6,6),(3,6,7),(3,6,8),(3,6,9),(3,6,10),(3,7,1),(3,7,2),(3,7,3),(3,7,4),(3,7,5),(3,7,6),(3,7,7),(3,7,8),(3,7,9),(3,7,10),(3,8,1),(3,8,2),(3,8,3),(3,8,4),(3,8,5),(3,8,6),(3,8,7),(3,8,8),(3,8,9),(3,8,10),(3,9,1),(3,9,2),(3,9,3),(3,9,4),(3,9,5),(3,9,6),(3,9,7),(3,9,8),(3,9,9),(3,9,10),(3,10,1),(3,10,2),(3,10,3),(3,10,4),(3,10,5),(3,10,6),(3,10,7),(3,10,8),(3,10,9),(3,10,10),(4,1,1),(4,1,2),(4,1,3),(4,1,4),(4,1,5),(4,1,6),(4,1,7),(4,1,8),(4,1,9),(4,1,10),(4,2,1),(4,2,2),(4,2,3),(4,2,4),(4,2,5),(4,2,6),(4,2,7),(4,2,8),(4,2,9),(4,2,10),(4,3,1),(4,3,2),(4,3,3),(4,3,4),(4,3,5),(4,3,6),(4,3,7),(4,3,8),(4,3,9),(4,3,10),(4,4,1),(4,4,2),(4,4,3),(4,4,4),(4,4,5),(4,4,6),(4,4,7),(4,4,8),(4,4,9),(4,4,10),(4,5,1),(4,5,2),(4,5,3),(4,5,4),(4,5,5),(4,5,6),(4,5,7),(4,5,8),(4,5,9),(4,5,10),(4,6,1),(4,6,2),(4,6,3),(4,6,4),(4,6,5),(4,6,6),(4,6,7),(4,6,8),(4,6,9),(4,6,10),(4,7,1),(4,7,2),(4,7,3),(4,7,4),(4,7,5),(4,7,6),(4,7,7),(4,7,8),(4,7,9),(4,7,10),(4,8,1),(4,8,2),(4,8,3),(4,8,4),(4,8,5),(4,8,6),(4,8,7),(4,8,8),(4,8,9),(4,8,10),(4,9,1),(4,9,2),(4,9,3),(4,9,4),(4,9,5),(4,9,6),(4,9,7),(4,9,8),(4,9,9),(4,9,10),(4,10,1),(4,10,2),(4,10,3),(4,10,4),(4,10,5),(4,10,6),(4,10,7),(4,10,8),(4,10,9),(4,10,10),(5,1,1),(5,1,2),(5,1,3),(5,1,4),(5,1,5),(5,1,6),(5,1,7),(5,1,8),(5,1,9),(5,1,10),(5,2,1),(5,2,2),(5,2,3),(5,2,4),(5,2,5),(5,2,6),(5,2,7),(5,2,8),(5,2,9),(5,2,10),(5,3,1),(5,3,2),(5,3,3),(5,3,4),(5,3,5),(5,3,6),(5,3,7),(5,3,8),(5,3,9),(5,3,10),(5,4,1),(5,4,2),(5,4,3),(5,4,4),(5,4,5),(5,4,6),(5,4,7),(5,4,8),(5,4,9),(5,4,10),(5,5,1),(5,5,2),(5,5,3),(5,5,4),(5,5,5),(5,5,6),(5,5,7),(5,5,8),(5,5,9),(5,5,10),(5,6,1),(5,6,2),(5,6,3),(5,6,4),(5,6,5),(5,6,6),(5,6,7),(5,6,8),(5,6,9),(5,6,10),(5,7,1),(5,7,2),(5,7,3),(5,7,4),(5,7,5),(5,7,6),(5,7,7),(5,7,8),(5,7,9),(5,7,10),(5,8,1),(5,8,2),(5,8,3),(5,8,4),(5,8,5),(5,8,6),(5,8,7),(5,8,8),(5,8,9),(5,8,10),(5,9,1),(5,9,2),(5,9,3),(5,9,4),(5,9,5),(5,9,6),(5,9,7),(5,9,8),(5,9,9),(5,9,10),(5,10,1),(5,10,2),(5,10,3),(5,10,4),(5,10,5),(5,10,6),(5,10,7),(5,10,8),(5,10,9),(5,10,10),(6,1,1),(6,1,2),(6,1,3),(6,1,4),(6,1,5),(6,1,6),(6,1,7),(6,1,8),(6,1,9),(6,1,10),(6,2,1),(6,2,2),(6,2,3),(6,2,4),(6,2,5),(6,2,6),(6,2,7),(6,2,8),(6,2,9),(6,2,10),(6,3,1),(6,3,2),(6,3,3),(6,3,4),(6,3,5),(6,3,6),(6,3,7),(6,3,8),(6,3,9),(6,3,10),(6,4,1),(6,4,2),(6,4,3),(6,4,4),(6,4,5),(6,4,6),(6,4,7),(6,4,8),(6,4,9),(6,4,10),(6,5,1),(6,5,2),(6,5,3),(6,5,4),(6,5,5),(6,5,6),(6,5,7),(6,5,8),(6,5,9),(6,5,10),(6,6,1),(6,6,2),(6,6,3),(6,6,4),(6,6,5),(6,6,6),(6,6,7),(6,6,8),(6,6,9),(6,6,10),(6,7,1),(6,7,2),(6,7,3),(6,7,4),(6,7,5),(6,7,6),(6,7,7),(6,7,8),(6,7,9),(6,7,10),(6,8,1),(6,8,2),(6,8,3),(6,8,4),(6,8,5),(6,8,6),(6,8,7),(6,8,8),(6,8,9),(6,8,10),(6,9,1),(6,9,2),(6,9,3),(6,9,4),(6,9,5),(6,9,6),(6,9,7),(6,9,8),(6,9,9),(6,9,10),(6,10,1),(6,10,2),(6,10,3),(6,10,4),(6,10,5),(6,10,6),(6,10,7),(6,10,8),(6,10,9),(6,10,10),(7,1,1),(7,1,2),(7,1,3),(7,1,4),(7,1,5),(7,1,6),(7,1,7),(7,1,8),(7,1,9),(7,1,10),(7,2,1),(7,2,2),(7,2,3),(7,2,4),(7,2,5),(7,2,6),(7,2,7),(7,2,8),(7,2,9),(7,2,10),(7,3,1),(7,3,2),(7,3,3),(7,3,4),(7,3,5),(7,3,6),(7,3,7),(7,3,8),(7,3,9),(7,3,10),(7,4,1),(7,4,2),(7,4,3),(7,4,4),(7,4,5),(7,4,6),(7,4,7),(7,4,8),(7,4,9),(7,4,10),(7,5,1),(7,5,2),(7,5,3),(7,5,4),(7,5,5),(7,5,6),(7,5,7),(7,5,8),(7,5,9),(7,5,10),(7,6,1),(7,6,2),(7,6,3),(7,6,4),(7,6,5),(7,6,6),(7,6,7),(7,6,8),(7,6,9),(7,6,10),(7,7,1),(7,7,2),(7,7,3),(7,7,4),(7,7,5),(7,7,6),(7,7,7),(7,7,8),(7,7,9),(7,7,10),(7,8,1),(7,8,2),(7,8,3),(7,8,4),(7,8,5),(7,8,6),(7,8,7),(7,8,8),(7,8,9),(7,8,10),(7,9,1),(7,9,2),(7,9,3),(7,9,4),(7,9,5),(7,9,6),(7,9,7),(7,9,8),(7,9,9),(7,9,10),(7,10,1),(7,10,2),(7,10,3),(7,10,4),(7,10,5),(7,10,6),(7,10,7),(7,10,8),(7,10,9),(7,10,10),(8,1,1),(8,1,2),(8,1,3),(8,1,4),(8,1,5),(8,1,6),(8,1,7),(8,1,8),(8,1,9),(8,1,10),(8,2,1),(8,2,2),(8,2,3),(8,2,4),(8,2,5),(8,2,6),(8,2,7),(8,2,8),(8,2,9),(8,2,10),(8,3,1),(8,3,2),(8,3,3),(8,3,4),(8,3,5),(8,3,6),(8,3,7),(8,3,8),(8,3,9),(8,3,10),(8,4,1),(8,4,2),(8,4,3),(8,4,4),(8,4,5),(8,4,6),(8,4,7),(8,4,8),(8,4,9),(8,4,10),(8,5,1),(8,5,2),(8,5,3),(8,5,4),(8,5,5),(8,5,6),(8,5,7),(8,5,8),(8,5,9),(8,5,10),(8,6,1),(8,6,2),(8,6,3),(8,6,4),(8,6,5),(8,6,6),(8,6,7),(8,6,8),(8,6,9),(8,6,10),(8,7,1),(8,7,2),(8,7,3),(8,7,4),(8,7,5),(8,7,6),(8,7,7),(8,7,8),(8,7,9),(8,7,10),(8,8,1),(8,8,2),(8,8,3),(8,8,4),(8,8,5),(8,8,6),(8,8,7),(8,8,8),(8,8,9),(8,8,10),(8,9,1),(8,9,2),(8,9,3),(8,9,4),(8,9,5),(8,9,6),(8,9,7),(8,9,8),(8,9,9),(8,9,10),(8,10,1),(8,10,2),(8,10,3),(8,10,4),(8,10,5),(8,10,6),(8,10,7),(8,10,8),(8,10,9),(8,10,10),(9,1,1),(9,1,2),(9,1,3),(9,1,4),(9,1,5),(9,1,6),(9,1,7),(9,1,8),(9,1,9),(9,1,10),(9,2,1),(9,2,2),(9,2,3),(9,2,4),(9,2,5),(9,2,6),(9,2,7),(9,2,8),(9,2,9),(9,2,10),(9,3,1),(9,3,2),(9,3,3),(9,3,4),(9,3,5),(9,3,6),(9,3,7),(9,3,8),(9,3,9),(9,3,10),(9,4,1),(9,4,2),(9,4,3),(9,4,4),(9,4,5),(9,4,6),(9,4,7),(9,4,8),(9,4,9),(9,4,10),(9,5,1),(9,5,2),(9,5,3),(9,5,4),(9,5,5),(9,5,6),(9,5,7),(9,5,8),(9,5,9),(9,5,10),(9,6,1),(9,6,2),(9,6,3),(9,6,4),(9,6,5),(9,6,6),(9,6,7),(9,6,8),(9,6,9),(9,6,10),(9,7,1),(9,7,2),(9,7,3),(9,7,4),(9,7,5),(9,7,6),(9,7,7),(9,7,8),(9,7,9),(9,7,10),(9,8,1),(9,8,2),(9,8,3),(9,8,4),(9,8,5),(9,8,6),(9,8,7),(9,8,8),(9,8,9),(9,8,10),(9,9,1),(9,9,2),(9,9,3),(9,9,4),(9,9,5),(9,9,6),(9,9,7),(9,9,8),(9,9,9),(9,9,10),(9,10,1),(9,10,2),(9,10,3),(9,10,4),(9,10,5),(9,10,6),(9,10,7),(9,10,8),(9,10,9),(9,10,10),(10,1,1),(10,1,2),(10,1,3),(10,1,4),(10,1,5),(10,1,6),(10,1,7),(10,1,8),(10,1,9),(10,1,10),(10,2,1),(10,2,2),(10,2,3),(10,2,4),(10,2,5),(10,2,6),(10,2,7),(10,2,8),(10,2,9),(10,2,10),(10,3,1),(10,3,2),(10,3,3),(10,3,4),(10,3,5),(10,3,6),(10,3,7),(10,3,8),(10,3,9),(10,3,10),(10,4,1),(10,4,2),(10,4,3),(10,4,4),(10,4,5),(10,4,6),(10,4,7),(10,4,8),(10,4,9),(10,4,10),(10,5,1),(10,5,2),(10,5,3),(10,5,4),(10,5,5),(10,5,6),(10,5,7),(10,5,8),(10,5,9),(10,5,10),(10,6,1),(10,6,2),(10,6,3),(10,6,4),(10,6,5),(10,6,6),(10,6,7),(10,6,8),(10,6,9),(10,6,10),(10,7,1),(10,7,2),(10,7,3),(10,7,4),(10,7,5),(10,7,6),(10,7,7),(10,7,8),(10,7,9),(10,7,10),(10,8,1),(10,8,2),(10,8,3),(10,8,4),(10,8,5),(10,8,6),(10,8,7),(10,8,8),(10,8,9),(10,8,10),(10,9,1),(10,9,2),(10,9,3),(10,9,4),(10,9,5),(10,9,6),(10,9,7),(10,9,8),(10,9,9),(10,9,10),(10,10,1),(10,10,2),(10,10,3),(10,10,4),(10,10,5),(10,10,6),(10,10,7),(10,10,8),(10,10,9),(10,10,10)]
We krijgen dan een lange lijst van tuples van alle mogelijke combinaties.
We gaan dit nu beperken naar een lijst van rechthoekige driehoeken met behulp van de stelling van Pythagoras.
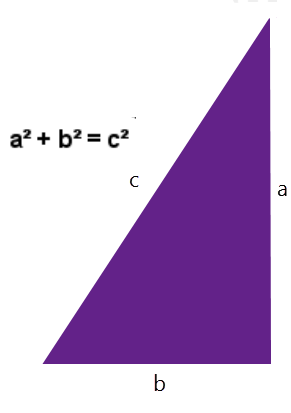
ghci> let triangles = [ (a,b,c) | a <-[1..10], b <-[1..10], c<-[1..10], a^2 + b^2 == c^2]
ghci> triangles
[(3,4,5),(4,3,5),(6,8,10),(8,6,10)]
Je ziet dat we na de komma een voorwaarde hebben gesteld met behulp van de stelling van Pythagoras. We kunnen nu dus vrij snel alle mogelijke rechthoeken tonen met zijde kleiner of gelijk aan 10.
Anders dan in een lijst is het in een tuple toegestaan om meerdere typen data te combinareren zoals bijvoorbeeld (1, "a"). Een tuple met 2 elementen noemen we een 2-tuple. Tuples met 3 elementen heten een 3-tuple etc.

