1. Wat is een automaat
Een automaat is een abstract model van een digitale computer of een bepaald systeem. Een computer of automaat heeft essentiële functies. De automaat heeft een mechanisme om input te kunnen lezen. In vroeger tijden was dat bij een computer bijvoorbeeld de invoer van ponskaarten. Vertaald naar een automaat houdt dit in dat de automaat kennis moet hebben over het gegeven alfabet. In het geval van de ponskaarten moet de computer de positie van de gaatjes kunnen lezen en weten wat deze betekenen.

Een ponskaart om de deur van een hotel te openen.
Een computer kan altijd maar één symbool tegelijk lezen en meestal wordt van links naar rechts gelezen. Er dient ook een mechanisme te zijn wat het einde van de string detecteert.
Een automaat produceert ook een output in één of andere vorm. Er kan ook sprake zijn van een tijdelijke opslag.
Soorten automaten
Een automaat kan dus worden gezien als een mechanisme wat strings kan herkennen. Een ander woord voor automaat is accepter. We zullen in de lesonderdelen hierna eindige automaat bestuderen. Dit is een automaat waar een string ingevoerd kan worden en dit leidt tot een eindtoestand. Een eindige automaat heeft altijd een aantal interne toestanden waaronder een begintoetsand. De begintoestand is de toestand waarin de automaat zich bevindt als er nog geen strings zijn ingevoerd.
Een automaat kan non-deterministisch of deterministisch zijn. Deterministisch houdt in dat een ingevoerde string maar op één manier kan worden gelezen. Het is gebruikelijk om deze twee automaten als een afkorting op te schrijven:
- een deterministische eindige automaat korten we af met dfa, van het Engelse deterministic finite automaton.
- een niet-deterministische eindige automaat korten we af met nfa, van het Engelse nondeterministic finite automaton.
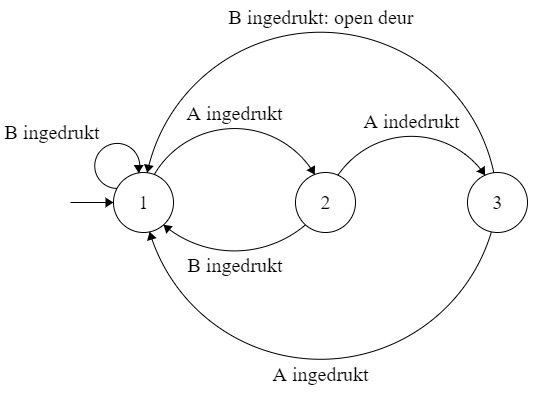
Een automaat voor toegangscontrole (bron: lessen over de Microbit)
2. Een automaat met JFlap
We zullen nu eerst via JFlap een eindige automaat maken. Open de tool en klik op Finite Automaton.
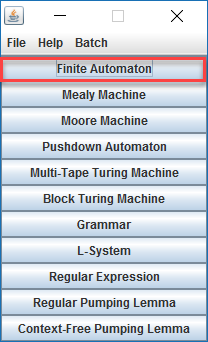
In het scherm hierna gaan we een eindige automaat maken in de vorm van een graaf. De grafentheorie is een tak van wiskunde die de eigenschappen van grafen bestudeert. Een graaf bestaat uit punten, deze worden knopen genoemd, die vaak zijn verbonden door lijnen. Als de lijnen pijlen worden dan spreken we van een gerichte graaf.
Maak drie toestanden (dit zijn dus de knopen van de graaf) q0, q1 en q2 met de State Creator.
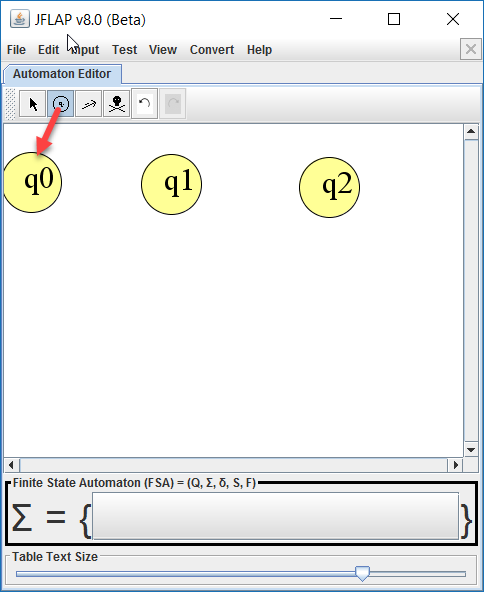
Maak overgangen (pijlen) met behulp van de Transition Creator.
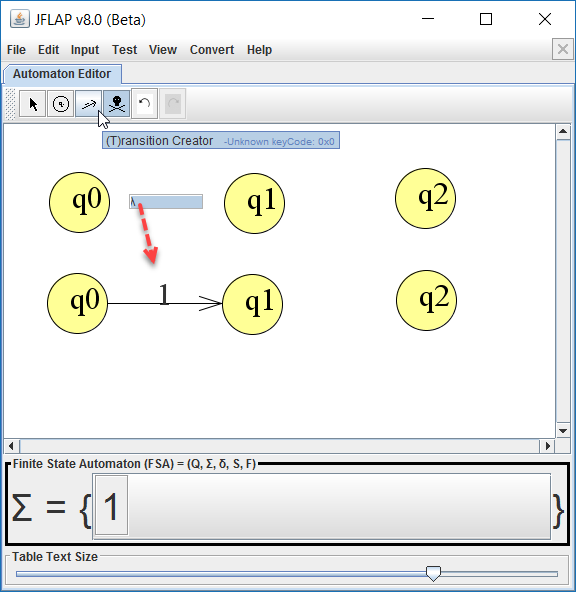
Uiteindelijk maak je alle overgangen als volgt:
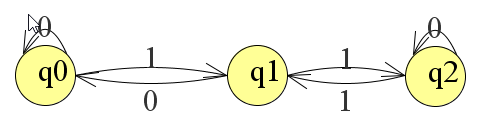
Als je een foutje maakt kun je met de Deleter of met Ctrl-Z het foutje ongedaan maken.
We hebben nu nog een begin- en eindtoestand nodig. Deze kun je maken door met de rechtermuisknop op een toestand te klikken.
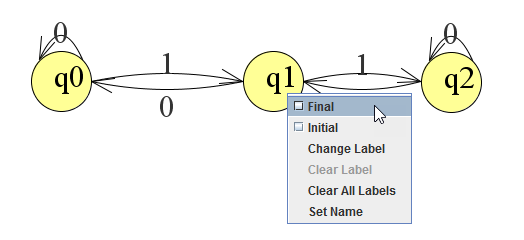
Uiteindelijk ziet de volledige automaat er zo uit:
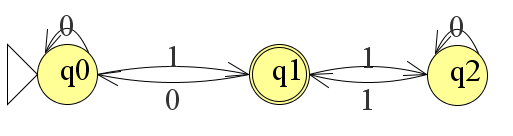
Wat heb je nu gemaakt? Een automaat die strings met 0-en en 1-en accepteert. We zullen dit demonstreren. Klik in het menu Input op Step with Closure..
Stel we hebben de volgende string: 10111. De automaat start in de begintoestand.
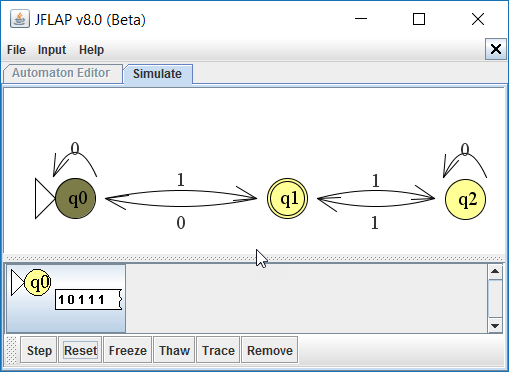
Vervolgens leest de automaat het eerste karakter: 1. De automaat komt in de toestand q1 vanwege de overgang die een 1 accepteert.
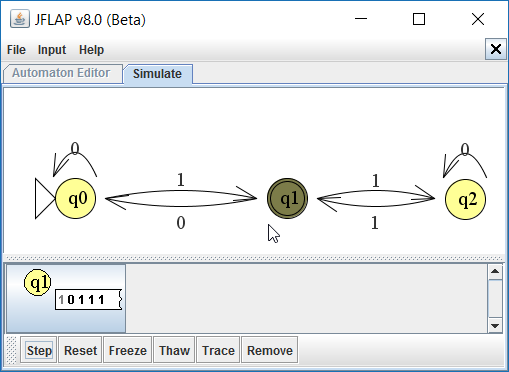
Bij het lezen van het 2e karakter, 0, komt de automaat weer terug in q0.
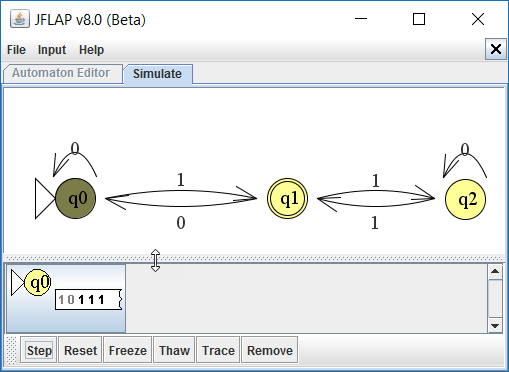
Bij het lezen van het derde karakter, een 1, komt de automaat opnieuw toestand q1. De laatste 2 karakters, twee keer een 1, brengt de automaat achtereenvolgens in toestand q2 en opnieuw weer in q1.
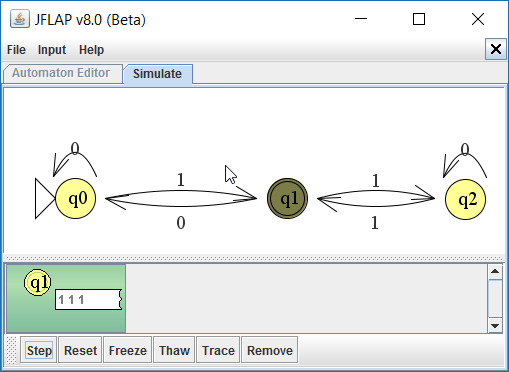
Je ziet dat de string wordt geaccepteerd omdat de automaat in q1 komt, de eindtoestand.
3. Met JFlap strings controleren in een automaat
In de opdracht van het vorige lesonderdeel moest je controleren of de automaat een bepaalde string accepteert. Dit kun je ook laten checken door JFlap. Als je de automaat hebt gemaakt kun je een string invoeren. Klik hiervoor onder input op Step with Closure.
In het navolgende veldje kun je de string invoeren.
Vervolgens kun je met de Step de string laten inlezen. Als de eindtoestand wordt bereikt, is de string geaccepteerd. Het veld van de ingevoerde string kleurt rood als deze niet wordt geaccepteerd.
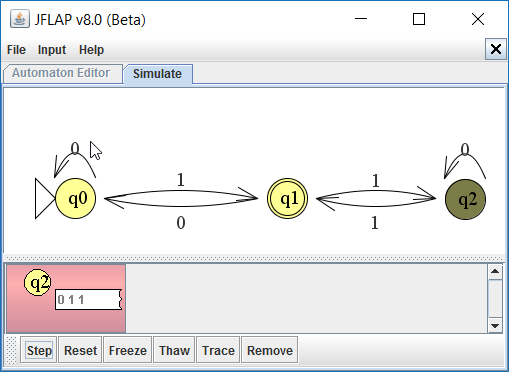
4. Een formele definitie voor een automaat.
We zijn nu ook in staat om een definitie te maken voor een automaat.
- Q is een eindig aantal sets van interne toestanden.
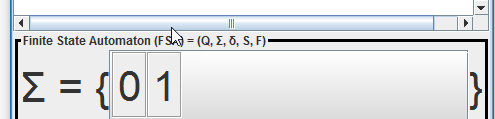
- ∑ is een verzameling van de input karakters. We noemen dit het invoeralfabet (input alphabet).
- δ (delta) staat voor alle overgangsfuncties (transition function).
- q0 is de begintoestand (initial state).
- F is de verzameling eindtoestanden (final states) en is dus een deelverzameling van Q. F kan gelijk zijn aan Q. Wiskundig schrijven we dat zo op: F ⊆ Q.
We kunnen nu de volledige automaat geven en geven deze de letter M.
M = {Q, ∑, δ, q0, F }
In JFlap heb je deze definitie misschien ook al gezien. q0 wordt daarin aangegeven met een S.
5. Een trap state
We zullen proberen de volgende grammatica uit te werken:
L={anb : n ≥ 0}
Deze grammatica produceert strings zoals ab, aab, aaab of b (n=0). Hoe kunnen we een automaat maken die deze strings, en alleen deze strings, accepteert?
We moeten in ieder geval een overgang maken die een oneindige hoeveelheid a-karakters kan lezen. Dat kan als volgt:
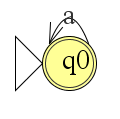
Deze automaat kan zowel een lege string als een oneindige hoeveelheid a-karakters. Merk op dat de begintoestand ook tevens de eindtoestand is.
We moeten nu echter ook de b kunnen lezen. Dit kan zo
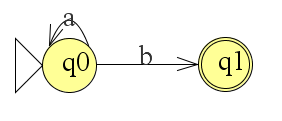
Waarbij we q1 als eindtoestand hebben ingesteld.
Je zou nu zeggen dat we klaar zijn maar als we de string aabb invoeren loopt de automaat in feite vast. Tot aab gaat het goed maar de b erna kan de automaat niet meer lezen. Hiervoor moeten we iets extra's maken en dat noemen we een trap state. Elke a of b die erna volgt moet ook kunnen leiden tot een toestand. We gaan deze leiden naar q2. De graaf die dan ontstaat ziet er als volgt uit:
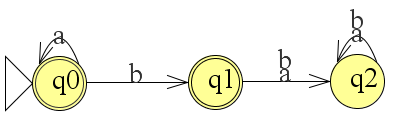
En is het mogelijk om elke string te lezen zonder dat de automaat vast loopt. We noemen dit een totale functie. Als we dus vragen om een totale automaat dan dien je ook rekening te houden met strings die geproduceerd kunnen worden die niet worden geaccepteerd maar die de automaat wel kan lezen.
6. Substrings herkennen
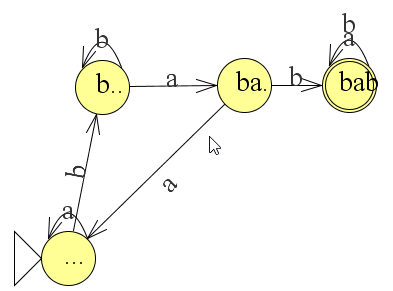
Een substring is een onderdeel van een string. In de string aabbab is "bab" een substring. Hoe kunnen we een automaat maken die de substring "bab" herkent? Door telkens een deel van de string te lezen en daarna weer terug te gaan naar de begintoestand. Als de substring wel wordt gelezen gaat de automaat naar de eindtoestand.
Formeel definiëren we deze taal als volgt:
L={x ∈ {a,b}* : x bevat de substring bab}
Het sterretje betekent: alle mogelijke strings die met a,b gemaakt kunnen worden.
We passen nu de volgende strategie toe. Zodra een string een b bevat springt de automaat in toestand b... . Vanaf hier wordt vanaf elke b nu gechecked of er een a met daarna een b volgt. Als dat zo is springt de automaat in de eindtoestand (invoer van a of b daarna maakt niet meer uit). Als dat niet zo is wordt opnieuw verwezen naar de begintoestand.
. 
7. Het complement van een automaat
In de laatste opgave hebben we een dfa gemaakt die de automaat precies omdraait. Deze accepteert alleen strings zonder sos. We noemen dit het complement van de taal L.
We konden dit bereiken door de eindtoestanden om te draaien. Dus de bestaande eindtoestand werd een gewone toestand en alle overige toestanden werden eindtoestanden. Er is een manier om dit op te schrijven.
De definitie van een automaat is:
M = {Q, ∑, δ, q0, F }
Alle toestanden waren: Q
De verzameling eindtoestanden zijn: F
Alle eindtoestanden omkeren schrijf je op met Q-F.
De defintitie wordt dus M' = {Q, ∑, δ, q0, Q-F }
Het complement geef je aan met een '.
8. Reguliere talen
Iedere eindige automaat accepteert een of andere vorm van een taal. Als je alle eindige automaten bij elkaar neemt kun je spreken van de familie van reguliere talen. Wanneer is een taal regulier? Antwoord: een taal is regulier als er een eindige automaat voor gevonden kan worden. We zullen dit aantonen met een voorbeeld.
Stel dat we de volgende taal hebben gedefiniëerd:
L = {awa : w ∈ {a,b}*}
Deze definitie geeft aan dat iedere string moet beginnen en eindigen met een a. Hoe gaan we daar een dfa voor maken in JFlap? We zullen dat stap voor stap uitleggen.
Begin met het maken van een splitsing. Als de string met een b begint kan de string niet worden geaccepteerd en kun je hier een trapstate voor maken.
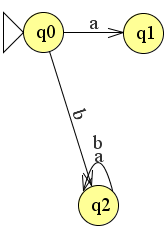
Nu je het beginkarakter hebt maakt het niet uit welke string er vervolgens wordt geconstrueerd.
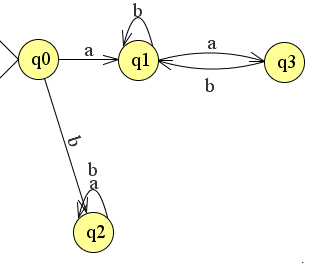
Als laatste moet er nog een constructie worden gemaakt om de automaat eindig te maken zodat alleen een string die eindigt op een a wordt geaccepteerd.
9. Antwoorden
opdracht 2.1
- 0001010101 100: niet geaccepteerd
- 0000010001: geaccepteerd
- 0000110001 1:niet geaccepteerd
Opdracht 2.2
Het antwoord is:
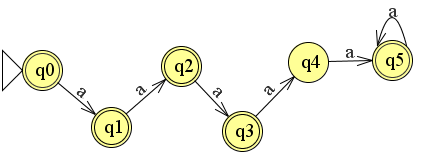
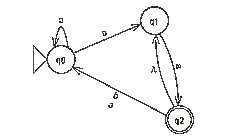
Het driehoekje q0 - q1 - q3 voegt weinig toe omdat de 0 ook via q0 - q3 in q3 terecht komt. q1 kunnen we dus verwijderen. Vanaf q3 levert zowel een 0 als een 1 de eindtoestand q5 op (en komt via de lambda ook weer terecht in q0 zodat je oneindig 0-en en 1-en kunt produceren). q2 en q4 voegen weinig toe en kunnen daarom veilig worden verwijderd.
De taal is{0n,1n: n>=1}
opdracht 3.1
00000000000000000001
01111111111111111111
of
111111111111111111111
opdracht 4.1
Het alfabet bestaat uit 0 en 1.
opdracht 5.1 t/m 5.5
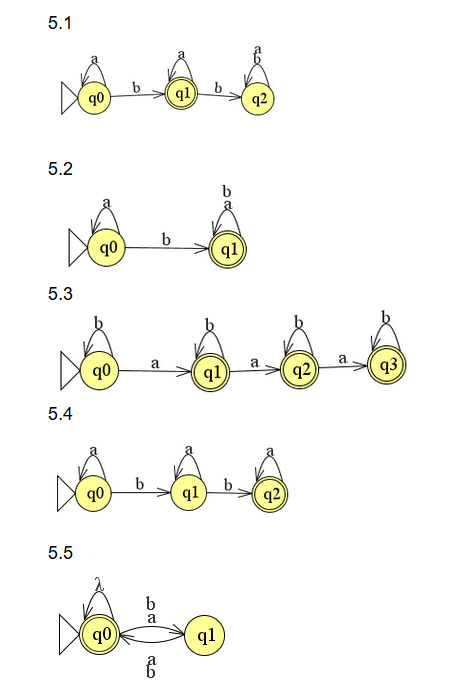
opmerking bij opdracht opdracht 5.3
Er wordt niet om een totale automaat gevraagd. De trapstate mag je dan achterwege laten. Verder is het antwoord niet goed. Toestand q0 moet ook final zijn.
opmerking bij opdracht opdracht 5.4
Ook hier wordt niet om een totale automaat gevraagd.
opdracht 6.1
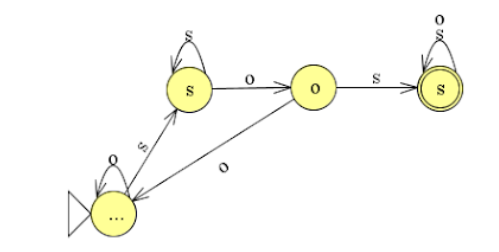
opdracht 6.2
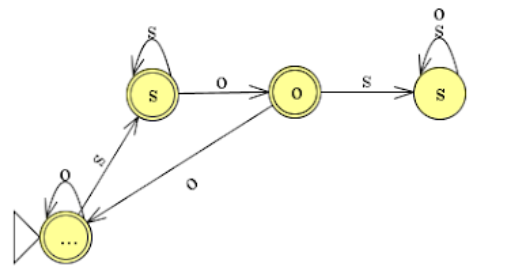
Hier worden dus de eindtoestanden omgedraaid.
opdracht 7.1
De substring die herkent wordt is 00
opdracht 8.1
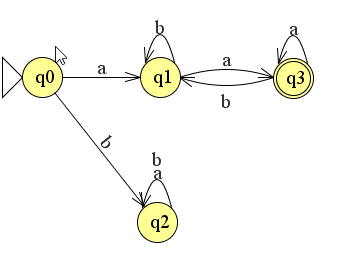
opdracht 8.2