1. oefenexamen/tentamen deel 1 en 2

vraag 1

Gegeven is de volgende taal:

L={w∈{a,b} : |w| ≤ 2 en |w| ≥ 4}. Geef de inverse van de taal en maak van deze taal vervolgens een automaat.

vraag 2

Gegeven is de volgende  L(G)={aⁿb^m : n ≥ 1, m > 2}

Geef de productieregels en de automaat. Het is toegestaan om JFlap te gebruiken maar niet op je examen.

vraag 3

Geef een voorbeeld van een automaat zoals die hede ten dage in de praktijk wordt gebruikt.

vraag 4

Hieronder zie je een gemaakte automaat in JFlap.

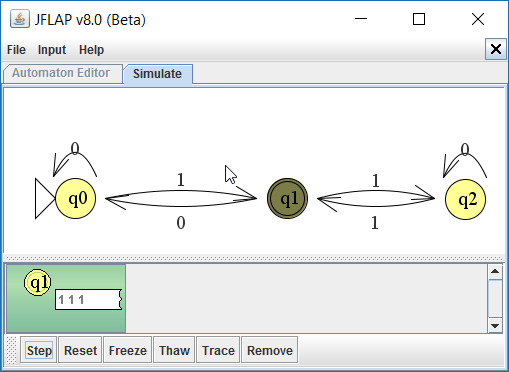
Geef de inverse van deze automaat.

vraag 5

Gegeven is de definitie van een automaat: M = {Q, ∑, δ, q0, F }

Leg in je eigen woorden uit wat deze symbolen betekenen (Dus het kopiëren van de tekst op edictum heeft geen zin. Je moet het in je eigen woorden kunnen uitleggen).

vraag 6

Maak een totale dfa (dus met een trap-state)  die strings met precies 2 a's accepteert voor ∑={a,b}. Maak vervolgens de productieregels.

vraag 7

Gegeven is L={x ∈ {a,b}* : x bevat de substring bbb}.

Maak deze automaat en de bijbehorende productieregels.

vraag 8

Laat zien dat de taal L={aⁿ : n ≥ 2, n ≠ 3} regulier is. D.w.z. verzin er een dfa voor.

vraag 9

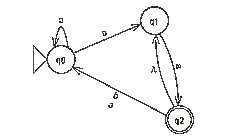
Gegeven is de volgende automaat.

Is deze automaat deterministisch? Motiveer je antwoord.

2. antwoorden vraag 1-3

vraag 1

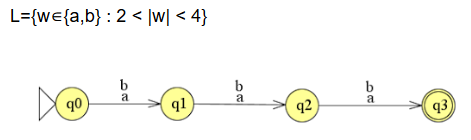
Oftewel |w|=3

vraag 2

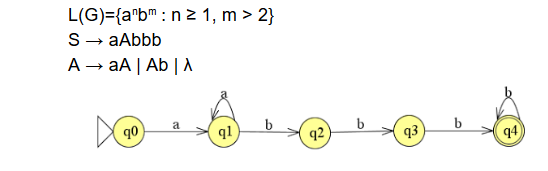
vraag 3

Bijvoorbeeld een frisdrankautomaat. Het ingooien van het geld is dan de string.

3. antwoorden vraag 4-9

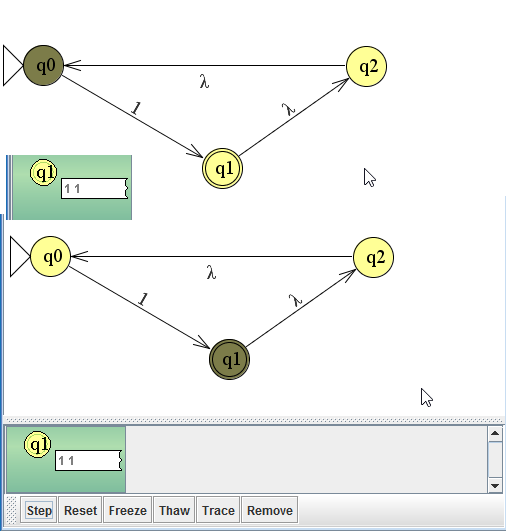
vraag 4

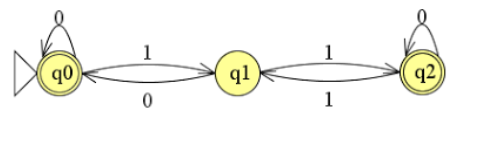
De inverse van een automaat is altijd het omdraaien van de final states.

vraag 5

• Q is een eindig aantal sets van interne toestanden, dus bij vraag 4 is dat {q0, q1, q2}.
• ∑ is een verzameling van de input karakters. We noemen dit het invoeralfabet (input alphabet). Dus als de verzameling is {a,b} kunnen er alleen strings worden gemaakt met a's en b's.
• δ (delta) staat voor alle overgangsfuncties dus bijvoorbeeld van q0 naar q1.
  
• q0 is de begintoestand (initial state).
  
• F is de verzameling eindtoestanden (final states) en is dus een deelverzameling van Q. F kan gelijk zijn aan Q. Wiskundig schrijven we dat zo op: F ⊆ Q. 

vraag 6

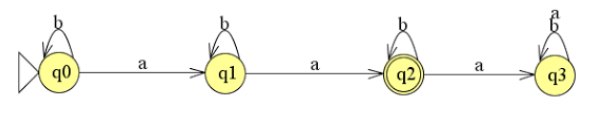
S → BaBaB

B → bB | b | λ

vraag 7

L={x ∈ {a,b}* : x bevat de substring bbb}.

 

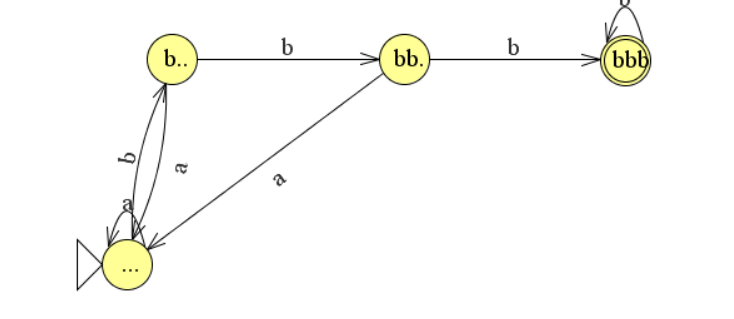
Productieregels:

S ->AbbbA

A->Aa | Ab | λ

vraag 8

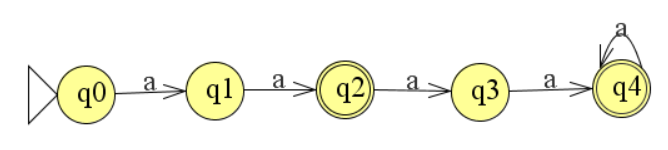
vraag 9

Nee, want zodra er een 1 wordt ingevoerd (er worden alleen maar enen geaccepteerd) zorgt de lambda ervoor dat deze via q2 weer terecht komt in q0. Het is dus een nfa.

4. tentamen deel 1 en 2

vraag 1 (10 punten)

Maak een automaat en een grammatica met precies 3 a's met x ∈ {a,b}*

vraag 2 (10 punten)

Maak een afleiding uit de volgende grammatica van minimaal 6 tekens.

S → aA

A → bS

S → λ

Definiëer de grammatica formeel, dus L(G)={ ......}. Zie deel 1 les 7 voor een voorbeeld.

vraag 3 (15 punten)

w∈{a,b}*.

Verzin de productieregels met de volgende restricties:

1. L(G)={aⁿb^n-3 : n ≥ 3 }

vraag 4 (10 punten)

Maak van vraag 3 een automaat. Waar loop je tegenaan?

vraag 5 (20 punten)

Mod betekent de restwaarde. Dus bijvoorbeeld 26 mod 8 = 2 omdat 3 x 8 = 24 en 26-24 = 2. Als er staat |w| mod 3 > 0 dan moet de restwaarde van de uitkomst dus groter zijn dan 0 als je de lengte van w deelt door 3.

Gegeven zijn de volgende talen:

1. L={w : |w| mod 3 > 0 }
2. L={w : |w| mod 3 = 0 

Waarbij geldt: w∈{a}*.

Geef de 2 sets productieregels.

aanwijzing: bedenk hoeveel waarden mod 3 > 0  kan opleveren.

vraag 6 (15 punten)

Gegeven is de verzameling {a,b}. Maak drie keer een automaat voor deze verzameling met waarbij strings gevormd kunnen worden uit {a,b}* met de volgende restricties:

1. niet meer dan 3 a's.
2. alle mogelijke strings met precies één a
3. alle mogelijke strings minimaal één a en precies twee b's.

vraag 7 (20 punten)

Gegeven is de verzameling {0,1}. Verzin een automaat voor de volgende regel:

De automaat kan alle mogelijk strings maken uit {0,1}* dus ook de lege string. Iedere 00 wordt echter onmiddellijk gevolgd door een 1. Dus 101, 0010, 0010011001 worden geaccepteerd maar 0001 (met 3 x 0) en 00100 (zonder laatste 1) niet. M.a.w. als er 00 in de string zit moet dat worden aangevuld met een 1.

aanwijzing: dit probleem kun je proberen op te lossen door eerst de hoofdautomaat te verzinnen die alleen de string 001 accepteert. Vervolgens ga je kijken of die automaat ook substrings kan produceren. Het niveau waarop je de puzzel kunt oplossen bepaalt uiteindelijk het aantal punten voor deze opgave.

5. antwoorden tentamen deel 1 en 2

Dit onderdeel is uitgeschakeld door de docent.

6. examen op moodle

Ga naar het examen op moodle.

Log in met behulp van Google (de rode knop).

Wacht tot op het bord het wachtwoord verschijnt.