1. Niet-deterministische eindige automaten
In dit deel zullen we de niet-deterministische automaten gaan bestuderen. We zullen daar vanaf nu de afkorting nfa (nondeterministic finite automaton) voor gebruiken zoals ook al in deel 2 is genoemd. Nfa's zijn complexere automaten. Bovendien lijken ze onzinnig. Toch zullen we zien dat ze erg nuttig kunnen zijn.
Normaal gesproken denk je aan een computer als een deterministische automaat, dus een apparaat wat maar op één manier een invoerstring kan behandelen. Bij een dfa heet dat een wandeling door de graaf. Deze wandeling kan maar op één manier gemaakt worden. Bij een nfa is dat niet zo. Het verschil met een dfa is dat de wandeling op meerdere manieren gemaakt kan worden. Zodra één wandeling leidt tot een eindtoestand, wordt de taal geaccepteerd.
Hieronder een voorbeeld van een nfa . Deze automaat leidt bij invoer van de string aaaa tot meerdere toestanden. Als één van deze toestanden leidt tot een eindtoestand, wordt de taal geaccepteerd.
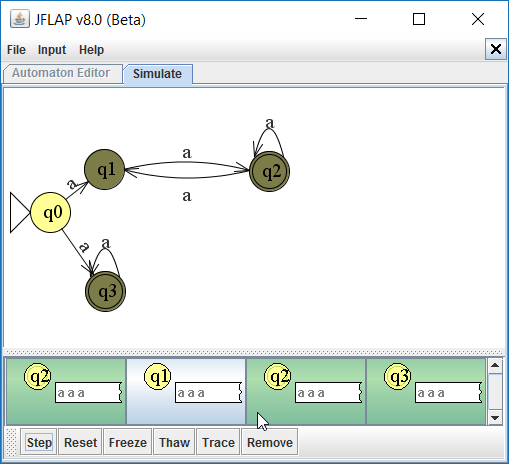
De string aaaa leidt tot meerdere eindtoestanden en wordt dus geaccepteerd.
2. De lambda overgang
De lambda is de 11e letter van het Griekse alfabet en schrijf je als λ. De λ staat voor lege string. Beschouw het volgende voorbeeld:
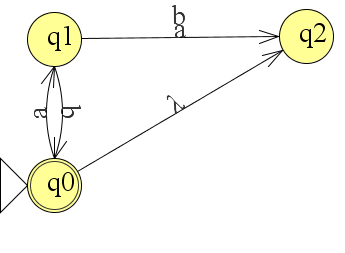
Bij invoer van de string abab springt de automaat meteen in twee toestanden. Je zou de string ook zo kunnen lezen λabab.
De eeste 2 toestanden zijn nu als volgt:
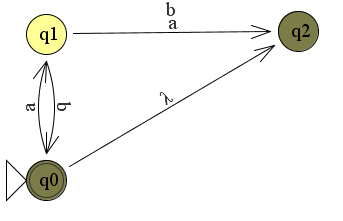
Dit is de situatie voordat de string is gelezen. De automaat maakt dus een keuze tussen q0 of q2.
Bij het lezen van de a loopt de automaat vast bij de overgang δ(q2, a). Dit is overigens de manier waarop je dit opschrijft. De overgang δ(q0, a) leidt tot q1. Kijk maar in onderstaand voorbeeld.
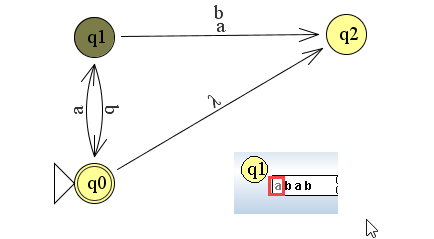
Bij het lezen van b zie je weer dezelfde beginsituatie ontstaan maar dit komt ook door de overgang δ(q1, b) = {q0, q2}

Uiteindelijk wordt de taal geaccepteerd omdat δ(q0, abab) leidt tot q0.
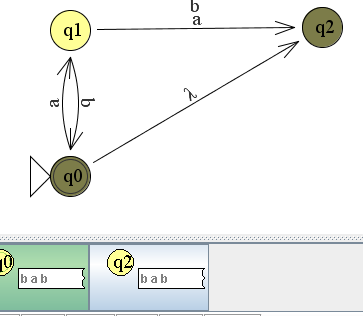
Met andere woorden:
De lambda-overgang wordt altijd gelezen en maakt dat een automaat in twee toestanden tegelijk komt. Uit de opdrachten zal het je waarschijnlijk nog duidelijker worden.
3. Van een nfa een dfa maken
Stel dat we de volgende nfa hebben gemaakt.
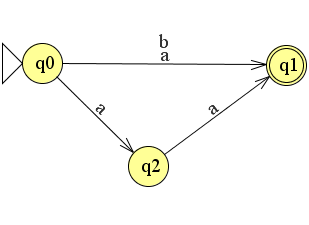
Hoe kun je zien dat het een nfa is? We zien dat als we de string a invoeren dat de automaat komt in twee toestanden: δ(q0, a) = {q1,q2}. Hieronder zullen we dit uitleggen o.a. aan de hand van een tabel:
Bij het lezen van de eerste a komt de nfa vanuit q0 in twee toestanden, namelijk q1 en q2. Dit schrijven we op in onderstaande tabel:
| lezen | toestanden |
q0 |
q1 |
q2 |
| a |
q1, q2 |
|
|
| b |
|
|
|
We kunnen dit als een dfa construeren door gewoon een nieuwe toestand te maken die we {q1,q2} noemen:
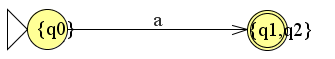
We maken dus van de verzameling {q1,q2} een nieuwe toestand en schrijven dit ook in de tabel. Merk op dat de nieuwe toestand {q1,q2} een eindtoestand is. Als in de originele nfa één van de twee toestanden een eindtoestand is dan is dat ook in de geconverteerde dfa.
We kunnen in JFlap de situatie {q1, q2} ook illustreren in de originele nfa:
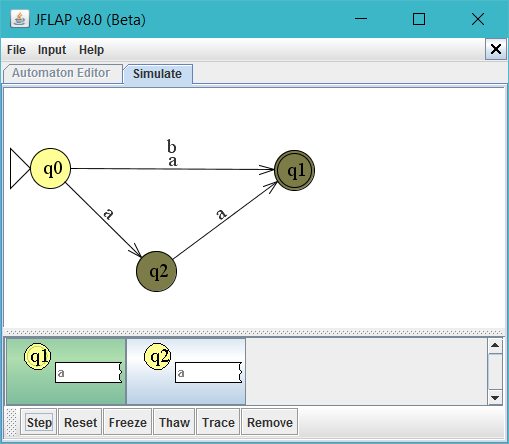
Nu gaan we verder. We kunnen ook een b invoeren. De automaat komt dan ook in de eindtoestand.
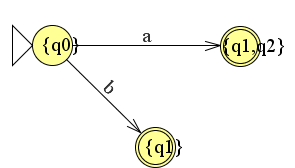
Dit schrijven we ook weer in de tabel.
| inlezen |
q0 |
q1 |
q2 |
| a |
{q1, q2} |
|
|
| b |
{q1} |
|
|
We moeten nu gaan kijken wat de automaat verder doet. Wat gebeurt er met een a vanuit zowel q1 als q2? Je moet dus in twee situaties tegelijk kijken. We zullen eerst in de tabel invullen wat er met een a gebeurt.
| inlezen |
q0 |
q1 |
q2 |
{q1, q2} |
| a |
{q1, q2} |
∅ |
{q1} |
{q1} |
| b |
(q1} |
|
|
|
Je neemt dus de verzameling van q1 en q2 en schrijft dat in een nieuwe kolom.
Met de b gebeurt het volgende:
| inlezen |
q0 |
q1 |
q2 |
{q1,q2} |
| a |
{q1, q2} |
∅ |
{q1} |
{q1} |
| b |
(q1} |
∅ |
∅ |
∅ |
Dit levert uiteindelijk bedoelde dfa op waarbij er dus geen pijl loopt voor bij vanuit {q1,q2} naar {q1}.
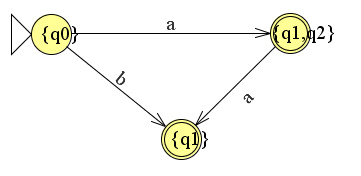
Merk ook op dat er in de tabel 3 overgangen staan. Dit is precies gelijk aan het aantal overgangen in de geconstrueerde dfa.
een moeilijker niveau
Stel dat we de volgende nfa hebben geconstrueerd:
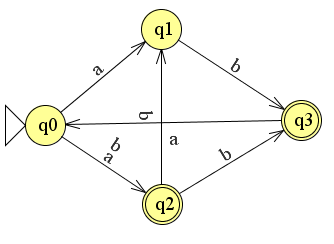
De opbouw van de bijbehorende tabel is als volgt:
| |
q0 |
q1 |
q2 |
q3 |
|
| a |
{q1,q2} |
|
|
|
|
| b |
{q2} |
|
|
|
|
| |
q0 |
q1 |
q2 |
q3 |
{q1,q2} |
| a |
{q1,q2} |
∅ |
∅ |
|
|
| b |
{q2} |
{q3} |
{q1,q3} |
|
{q1,q3} |
Let er goed op de letters aan de onderkant staan van de pijlen. Dus vanaf q2 komt de b terecht in q1 en q3.
Hier hoort nu de volgende automaat bij.
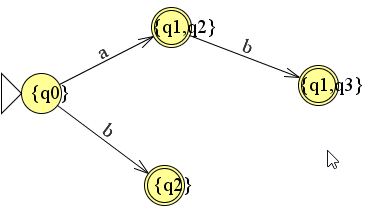
We kunnen nu in de kolom ook kijken wat er met de nieuwe situatie {q1,q3) gebeurt en we maken tevens de tabel verder af.
| |
q0 |
q1 |
q2 |
q3 |
{q1,q2} |
{q1,q3} |
| a |
{q1,q2} |
∅ |
∅ |
{q3} |
∅ |
{q0} |
| b |
{q2} |
{q3} |
{q1,q3} |
∅ |
{q1,q3} |
{q3} |
En we tekenen de volledige automaat.
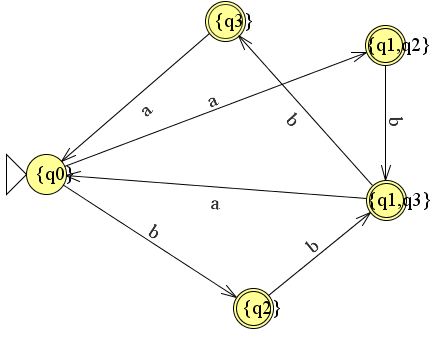
4. Reguliere expressies
Een andere manier om reguliere talen te beschrijven zijn reguliere expressies. Een reguliere expressie is een combinatie van een of andere alfabet Σ, haakjes en de operatoren +, . en *.
De . operator
Deze operator verbindt twee strings. Voorbeeld (a.b) = ab. We spreken af dat we deze operator in principe niet schrijven dus ab is hetzelfde als a.b.
De + operator
Deze operator maakt van twee strings de vereniging dus a + b = {a} ∪ {b} = {a,b}. De strings die geproduceerd kunnen worden zijn a of b. Lees plus als of.
Stel dat we de reguliere hadden gemaakt met een Kleene closure, dus (a + b)* dan krijg je de taal {a,b}*. Deze taal produceert een oneindig aantal a's en/of b's of een lege string dus L = {λ, a, b, aa , ab , bb , ba, aaa…….}
De lege taal
c + ∅ = {} ∪ {c} = de taal {c}. Strings die geproduceerd kunnen worden zijn c of niets.
De lege string
c + λ = {λ} ∪ {c} = de taal {λ,c}*. Strings die geproduceerd kunnen worden zijn λc (ook op te schrijven als c), cλ (ook op te schrijven als c), c of λ (op te schrijven als de lege string)
Leeg is dus iets anders dan een string waar niets in staat.
meer voorbeelden
a+b ={a} ∪ {b} en dat geeft L={a,b}.
a + b* = {a} ∪ {b}*. Stel de verzameling {b}* zo voor {λ, b, bb, bbb, bbbb, bbbbb.....} dus {a} ∪ {b}* wordt {a,b,bb,bbb,bbbb.......}. Formeel opgeschreven is dat dus {anbm: n=1 of m ≥ 0}
(ab)*ab = ab of abab of ababab dus minimaal één keer ab. {(ab)nab : n ≥ 0}
(0 + 10*) maakt L = { 0, 1, 10, 100, 1000, 10000, … }. Hier dus weer kiezen tussen 0 of 10*.
(0 + λ)(1 + λ) maakt L = {λ, 0, 1, 01}
5. Van reguliere expressie naar automaat
We hebben de volgende reguliere expressie gemaakt: a(ab)*. Welke automaat zou hierbij kunnen horen? We zullen deze stapsgewijs maken.
De reguliere expressie kan óf het stukje aan de rechterkant teruggeven. Dat is de lege string) of het stukje aan de linkerkant wat minimaal één a oplevert en nul of meerdere keren ab. Dit levert de volgende automaat op:

We kunnen de reguliere expressie uitbreiden door er bijvoorbeeld een b bij te plakken": a(ab)*b. Dit levert de volgende automaat op.
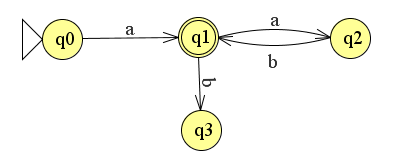
Merk op dat als je kiest voor een laatste (2e) b de automaat niet in Final State terecht komt.
6. van automaat naar reguliere expressie
Je kunt ook andersom rekenen; van automaat naar reguliere expressie. Dit kun je doen door de automaat als het ware te vereenvoudigen. Stel we hebben de volgende eindige automaat:
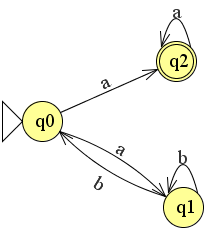
We kunnen deze vereenvoudigen door de lus q0 naar q1 te verwijderen en als het ware om te zetten naar een reguliere expressie.
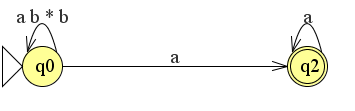
De automaat wordt nu al een stuk eenvoudiger. We kunnen nu al de reguliere expressie maken. We stellen het volgende:
r1 = q0 naar q0 = ab*b
r2 = q0 naar q2 = a
r3 = q2 naar q2 = a*
De reguliere expressie is nu r1*r2r3. Nu hoeven we alleen nog maar de reguliere expressies van de automaat over te nemen. De uiteindelijke reguliere expressie is nu (ab*b)*aa*.
iets ingewikkelder
We breiden de automaat nu uit met een extra verbinding van q1 naar q2.
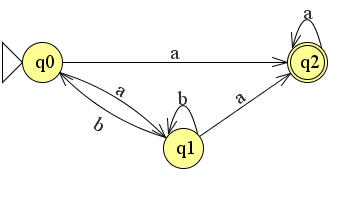
We hebben nu nog een pad gevonden die we moeten weghalen om q1 te verwijderen namelijk het pad q0 naar q1 naar q2. We hadden hierboven ook al het pad van q0 naar q1 en terug gevonden. Het vervangen van deze twee paden en het verwijderen van q1 levert het volgende plaatje op:
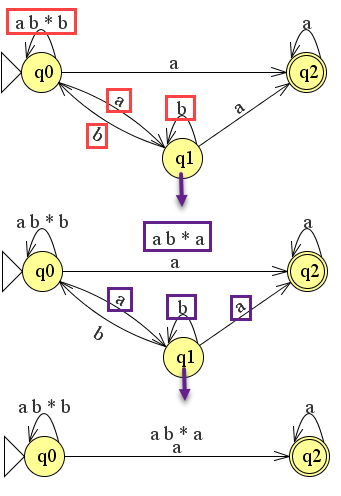
Je kunt nu opnieuw weer expressie onderscheiden:
r1 = q0 naar q0 = ab*b
r2 = q0 naar q2 = a óf
r3 = q0 naar q2 = ab*a
r4 = q2 naar q2 = a*
De reguliere expressie is grotendeels hetzelfde. Het verschil zit in het extra pad wat in r3 is benoemd.
r1* (r2 + r3) r4
Invullen van de expressies levert de uiteindelijke reguliere expressie op.
(ab*b)*(a + (ab*a))a*
7. links- en rechtslineaire grammatica
We kunnen een grammatica linkslineair of rechtslineair beschrijven. Een grammatica is rechtslineair als het is van de volgende vorm:
S → aS | λ
Dat houdt dus in dat alleen aan de rechterkant van de string karakters worden bijgevoegd dus aaa, aaaa etc.
Een linkslineaire grammatica is van de volgende vorm:
S → Sa | λ
Dan wordt aan de linkerkant van de strings karakters bijgevoegd dus aa, aaa, aaaa etc.
meer voorbeelden
We hebben de volgende grammatia G = ({S, A, B}, {a,b}, S, P) waarbij voor P geldt:
S → Aa | Ba
A → Ba | λ
B → Ab | λ
Deze grammatica levert de volgende strings op:
Aa ⇒ Baa ⇒ Abaa ⇒ Babaa ⇒ Ababaa ⇒ babaa
Je ziet dat er telkens aan de linkerkant karakters worden toegevoegd. Afhankelijk van de keuze die aan het begin wordt gemaakt kunnen de strings worden:
bababababaa of bababababa.
We kunnen dit voorbeeld ook rechtslineair laten zien:
S → aA | aB
A → aB | λ
B → bA | λ
8. Lambda verwijderen
We geven de volgende grammatica:
S → ABC
A → aA | λ
B → aB | λ
C → aC | λ
Dit is eigenlijk geen gewenste situatie. De grammatica (je kunt ook lezen - het programma) moet nu bij ieder hulpsymbool A, B of C controleren of er een lege string wordt geconstrueerd. Dat is niet erg efficiënt. Er is betere en snellere equivalente grammatica zonder lambda. Hoe kunnen we dat bereiken ? Dat gaat als volgt. Vraag jezelf af bij welke regels het hulpsymbool (A,B,C) verdwijnt doordat in de productieregels kan worden gekozen voor lambda.
We beschouwen de startproductieregel S → ABC
En de productieregel A → aA| λ
De afleiding kan dan worden S ⇒ aBC, S ⇒ aaBC etc. maar ook λBC⇒BC waarbij de A dus verdwijnt vanwege de lambda in bovenstaande productieregel
Dat is in bovenstaande grammatica bij alle hulpsymbolen A,B en C het geval. Je schrijft dat zo op: Variablenull=Vn={A,B,C,S}. Waarom zit S daar ook bij? Omdat S ook kan verdwijnen als je bij álle hulpsymbolen lambda kiest.
Nu ga je van deze verzameling alle mogelijke combinaties maken waaarbij telkens één van de hulpsymbolen uit de verzameling verdwijnt. Als volgt:
S → ABC|AB|AC|BC|A|B|C|λ
Merk op dat S op deze manier ook kan verdwijnen.
Nu moeten er nog drie productieregels bij om de taal equivalent te krijgen met de oorspronkelijke taal. Welke zijn dat? Deze mag je in de opdracht er zelf bijmaken. Ontdek daarbij dat deze grammatica precies dezelfde taal genereert als de oorspronkelijke grammatica.
9. Ketenvrij maken
Beschouw de volgende grammatica
S → aA | B
A → a | bb | B
B → a | bc| A
Hierin zit een keten die als is als volgt: S ⇒ B ⇒ A ⇒ B ⇒ A etc. Alhoewel dit uiteindelijk wel tot een productie kan leiden kan deze weg korter. We kunnen dit daarom beter verwijderen. We zullen dit ook nog eens aantonen met een graaf.
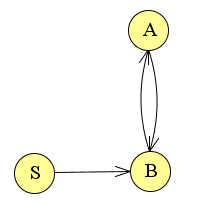
De keten is, zoals eerder is aangetoond: S ⇒ B ⇒ A
Het best kun je rechts van de keten beginnen. Dus A eerst verwijderen en de afleiding ervoor in de plaats schrijven:
S → aA | B
A → a | bb | B
B → a | bc | a | bb | B
Je ziet dat we a nu dubbel hebben dus dat mogen we verwijderen.
S → aA | B
A → a | bb | B
B → a | bc | bb | B
Daarna gaan we door met B. Omdat B ook naar zichzelf leidt mag dit worden verwijderd. Strict genomen moeten we de afleiding ervoor weer in de plaats schrijven maar dit leidt alleen maar tot dubbele afleidingen of een afleiding naar zichzelf (B → a | bc | bb | B | a | bc | bb | B). We komen daarom tot de volgende grammatica:
S → aA | B
A → a | bb | a | bc | bb
B → a | bc | bb
We verwijderen weer alle dubbele eindsymbolen dus uiteindelijk blijft over.
S → aA | B
A → a | bb | bc |
B → a | bc | bb
Omdat S ook in de keten zit zullen we hier ook nog mee aan de slag moeten. S leidde tot B dus die verwijderen dus dat schrijven we weer ervoor in de plaats.
S → aA | a | bc | bb
A → a | bb | bc |
B → a | bc | bb
Je kunt nu zien dat B niet meer bereikbaar is. We mogen deze daarom verwijderen in de uiteindelijke grammatica.
S → aA | a | bc | bb
A → a | bb | bc
10. De Chomsky normaalvorm
Het verwijderen van de lambda en het ketenvrij maken noemen we normaliseren. We kunnen hierin nog een stapje verder gaan door te normaliseren met de Chomsky normaalvorm. De Chomsky normaalvorm heeft alleen productieregels van de volgende vorm:
S → AS : maximaal 2 hulpsymbolen óf
S → a : maximaal één eindsymbool
Voorbeeld:
We geven de volgende productieregels:
S → ABa
A → aab
B → Ac
Om deze productieregels om te kunnen zetten in een Chomsky normaalvorm hanteren we de volgende regels:
- Verwijder alle lambdaproducties.
- Verwijder alle ketens
- Vervang alle karakters van strings met meer dan één eindsymbool of hulpsymbool door nieuwe hulpsymbolen voor de eindsymbolen.Begin hierbij achteraan in het alfabet dus abcd wordt WXYZ.
- Splits alle hulpsymbolen van meer dan 2 strings op door nieuwe hulpsymbolen in te voeren. Begin hierbij ook achteraan in het alfabet bij het symbool wat nog niet is gebruikt.
Dus:
Stap 1: in bovenstaande productieregels zijn geen lambda's dus deze stap slaan we over.
Stap 2: We zien bij de productieregel B → Ac een keten van S ⇒ B ⇒ A . De nieuwe productieregels worden daarom:
S → ABa
A → aab
B → aabc
stap 3: We vervangen nu alle afleidingen met meer dan 1 eindsymbool door nieuwe hulpsymbolen. Voor a schrijven we X, voor b schrijven we Y en voor c schrijven we Z.
S → ABX
A → XXY
B → XXYZ
X → a
Y → b
Z → c
stap 4: We splitsen alle strings met meer dan 2 hulpsymbolen op door nieuwe hulpsymbolen in te voeren. We werken hierbij van boven naar onder en we beginnen achteraan in het alfabet voor de nieuwe hulpsymbolen die van het alfabet nog niet zijn gebruikt. Voor BX schrijven we dus W.
S → AW
W → BX
De productieregel A → XXY splitsen we door voor XY de V te kiezen.
A → XV
V → XY
Als laatste nog het opsplitsen van B → XXYZ. Dit moet in twee stappen. Voor XYZ schrijven we de U:
B → XU
U → XYZ
Voor YZ schrijven we de V:
B → XU
U → XV
V → YZ
Waarmee we uiteindelijk de complete Chomsky normaalvorm kunnen geven:
S → AW
W → BX
B → XU
U → XV
V → YZ
X → a
Y → b
Z → c
11. antwoorden
opdracht 1.1
Zie les
opdracht 1.2
Deze opdracht kun je zelf controleren met Jflap. Wordt de lambda geaccepteerd? Wat hoort tot het alfabet?
opdracht 1.3
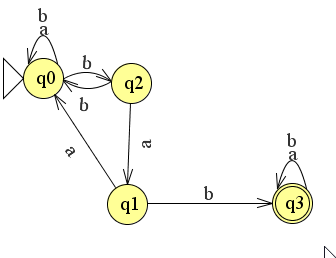
opdracht 2.1
| 1 |
Accept |
| 1 1 |
Accept |
| 1 1 1 |
Accept |
| λ |
Reject |
Dus een onbeperkte hoeveelheid 1-en waarbij geld dat er minimaal één 1 wordt geproduceerd.
opdracht 2.2
Uiteindelijk hou je onderstaande automaat over:
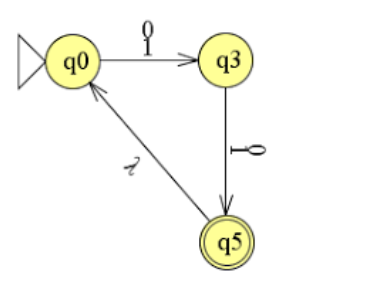
opdracht 2.3
Nee, deze automaat is niet deterministisch. Bij een dfa kan de string maar op één manier worden gelezen.
opdracht 3.1
Eerst maak je de volgende tabel:
Vervolgens ga je kijken vanuit welke toestand met een a of een b wordt gelezen en waar deze dan in terecht komt dus:
- Vanuit q0 kom je met een a in q1, en met een b in q1,q2
- vanuit q1 kom je met een a in q1 en q2
- en zo ga je door...
- de finale toestand markeren we met een kleur.
|
q0 |
q1 |
q2 |
| a |
q1 |
q1,q2 |
q1 |
| b |
q1,q2 |
- |
- |
In de tabel kun je nu drie toestanden onderscheiden namelijk q0 (begintoestand, die we altijd erbij betrekken), q1 en de nieuwe toestand q1,q2. Als je nu precies de tabel volgt dan krijg je de volgende automaat:

opdracht 4.1
- a + b => a of b
- a + bc => a of bc
- (a + b)* =>(a+b)(a+b)(a+b)(a+b)(a+b)(a+b)....=>bijvoorbeeld aaabbb
- a∅=>∅
- (a∅)a=>∅a=>∅
- aλb=>ab
- (a + bc)*(c + ∅)=>(a + bc)*c=>ac, bcc, aac, bcbcc etc.
- (a + b)c*=>accccc of bccccc of abcccc etc.
- (a+b)(a+b)=>aa, ab, bb, ba Merk op dat deze string even is.
opdracht 4.2
- ((a+b)*a(a+b)*) heeft de volgende strings: a, aa, ab, ba
- Als de string groter is dan 2 karakters dan is het aantal strings oneindig - de bovenste vier.
opdracht 4.3
(aa)*b(bb)*
opdracht 4.4
(a +b)*(a+bb) levert de volgende strings op: {a, bb, aa, abb, aabb, aaa}. Een andere verzameling is ook mogelijk.
opdracht 4.5
aaaa*(bb)*
opdracht 4.6
- (a + λ)* wordt a*
- aa* + λ wordt aa*
- (λ + a)(a + b)*(λ + a) wordt a(a+b)*a
- (a + b + ab + ba)* wordt (a+b)*
opdracht 4.7
Deze vraag wordt niet beantwoord en mag je zelf proberen te bedenken.
opdracht 5.1
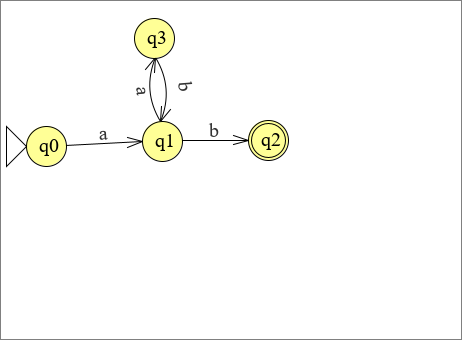
opdracht 5.2

opdracht 3.6.1
Je mag er in eerste instantie een nfa van maken. Evt. kun je daar weer een dfa van maken. Dat staat niet in de opdracht maar voor de volledigheid geven we deze erbij. Je ziet dat het veel lastiger is om bij een dfa de relatie te zien tussen de expressie en de automaat.

Opdracht 3.7.1
S ⇒ aA ⇒ aaB ⇒ aabA ⇒ aabaB ⇒ aaba
S ⇒ aB ⇒ abA ⇒ abaB ⇒ ababA ⇒ abab
Opdracht 3.7.2
Rechtslineair
S → abbA
A → aA | bA | lambda
Linkslineair
S → Aabb
A → Aa | Ab | lambda
opdracht 8.1
Bedenk wat er gebeurt als λ zou worden gebruikt.
S → ABC|AB|AC|BC|A|B|C|λ
A → aA | a
B → aB | a
C → aC | a
opdracht 8.2
Uiteindelijk houden we alleen de volgende grammatica over:
S → aSb|λ
opdracht 8.3
S -> U | UCU | λ
U -> AB | A | B
A -> a | aA
B -> bB
C -> cc
opdracht 9.4
Eerst zoek je de keten. Dat is S - B - A. Dit ga je eerst vervangen.
S → AB
A → aA | λ
B → bB | aA| λ
Hierbij heb je dus de inhoud van A bij B opgeschreven waar eerst een enkele A stond. Nu heb je de keten verwijderd.
Nu nog de lambda verwijderen waarbij we afspreken dat de S wel een lambda mag bevatten.
S → AB | A | B | λ
A → aA | a
B → bB | aA| b
opdracht 10.1
S → aSb|ab
stap 1 en 2 kunnen we overslaan omdat er geen ketens of lambda's zijn.
stap 3:
S → XSY
S → XY
X → a
Y → b
stap 4, opsplitsen. SY wordt W
S → XW
S → XY
W → SY
oftewel
S → XW | XY
W → SY
X → a
Y → b